Решебник по геометрии 9 класс Атанасян ФГОС Задание 1397

\[\boxed{\mathbf{1397.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

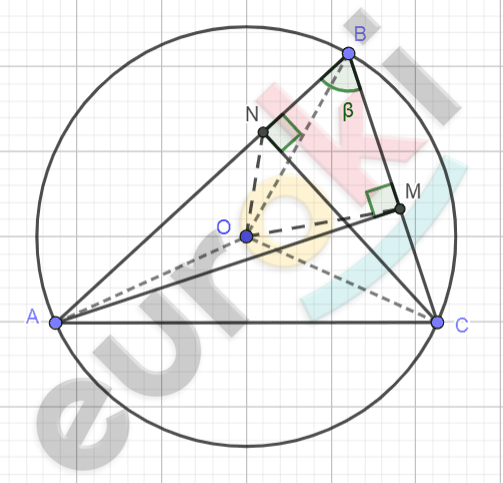
\[\mathrm{\Delta}ABC - остроугольный;\ \]

\[AB > BC,\ AM,\ CN - высоты;\]

\[O(O,\ R) - описанная\ \]

\[окружность;\ \]

\[\angle ABC = \beta;\ \]

\[S_{\text{NOMB}} = S.\]

\[Найти:\]

\[AC - ?\]

\[Решение.\]

\[1)\ Соотношение\ стороны\ \text{AC}\ \]

\[и\ синуса\ угла\ \beta:\ \]

\[\frac{\text{AC}}{\text{sinβ}} = 2R \Longrightarrow AC = 2R \cdot sin\beta.\]

\[Площадь\ четырехугольника\ \]

\[NOMB:\]

\[S_{\text{NOMB}} = S_{\text{OBN}} + S_{\text{OBM}}.\]

\[2)\ У\ \ треугольников\ \mathrm{\Delta}OBN\ \]

\[и\ \mathrm{\Delta}OBA\ одна\ высота \Longrightarrow\]

\[\Longrightarrow их\ площади\ \]

\[соотносятся\ как\ основания:\ \]

\[\frac{S_{\text{OBN}}}{S_{\text{OBA}}} = \frac{\text{NB}}{\text{AB}}\text{.\ }\]

\[Аналогично\ для\ \mathrm{\Delta}OBM\ и\]

\[\ \mathrm{\Delta}OBC:\]

\[\frac{S_{\text{OBM}}}{S_{\text{OBC}}} = \frac{\text{BM}}{\text{BC}}.\]

\[3)\ Получаем:\]

\[S_{\text{NOMB}} = \frac{\text{NB}}{\text{AB}}S_{\text{OBA}} + \frac{\text{BM}}{\text{BC}}S_{\text{OBC}};\]

\[S_{\text{OBA}} = \frac{1}{2}R^{2} \cdot sin2C,\ \ \]

\[\ S_{\text{OBC}} = \frac{1}{2}R^{2}sin2A.\]

\[4)\ \mathrm{\Delta}AMB\sim\mathrm{\Delta}CNB - по\ двум\ \]

\[углам:\]

\[\angle AMB = \angle CNB;\]

\[\angle B - общий.\]

\[\Longrightarrow \frac{\text{AB}}{\text{CB}} = \frac{\text{MB}}{\text{NB}}.\]

\[5)\ По\ теореме\ синусов:\]

\[\frac{\text{AB}}{\text{CB}} = \frac{\text{sinC}}{\text{sinA}}\]

\[BM = NB\frac{\text{sinC}}{\text{sinA}} = AB\ cos\beta\]

\[\frac{\text{NB}}{\text{AB}} = \frac{\text{sinA}}{\text{sinC}}cos\beta;\ \ \]

\[\frac{\text{BM}}{\text{BC}} = \frac{\text{AB\ cosβ}}{\text{BC}} = \frac{\text{sinC}}{\text{sinA}}\text{cosβ.}\]

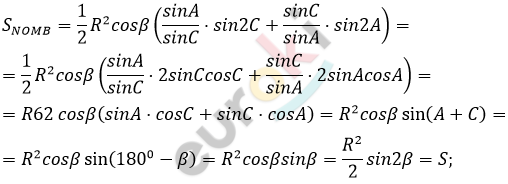
\[R^{2} = \frac{2S}{sin2\beta}.\]

\[6)\ AC = 2R \cdot sin\beta =\]

\[= 2\sqrt{\frac{2S}{sin2\beta}}sin\beta =\]

\[= 2\sqrt{\frac{2Ssin^{2}\beta}{2sin\beta\ cos\beta}} = 2\sqrt{\text{Stgβ}}.\]

\[Ответ:AC = 2\sqrt{\text{Stgβ}}.\]