Решебник по геометрии 9 класс Атанасян ФГОС Задание 1396

\[\boxed{\mathbf{1396.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[ABCD - трапеция,\ \]

\[AD||BC;\ \]

\[AD < BC;\ \]

\[AD = 3;\ \]

\[AB\bot BC;\ \]

\[CD = 6;\]

\[E \in CD;\ \]

\[EC = ED;\ \]

\[\angle CBE = a.\]

\[Найти:\]

\[S - ?\]

\[Решение.\]

\[1)\ Опустим\ перпендикуляры\ \]

\[DH\bot BC,\ EK\bot BC,\ \left\{ H,K \right\} \in BC.\]

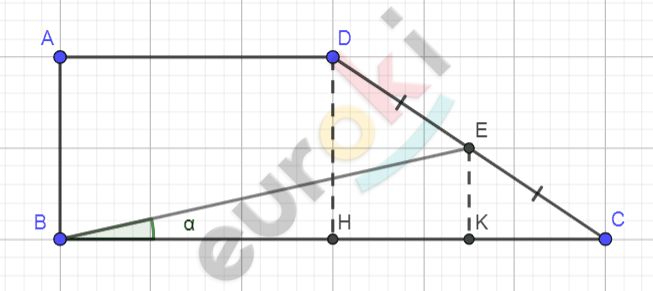
\[\left. \ \begin{matrix} \angle DHC = \angle EKC = 90{^\circ} \\ \angle C - общий\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right\} \Longrightarrow\]

\[\Longrightarrow \mathrm{\Delta}DHC\sim\mathrm{\Delta}EKC - по\ двум\ \]

\[углам.\]

\[Коэффициент\ подобия:\]

\[k = \frac{\text{CD}}{\text{CE}} = 2.\]

\[\ EK - средняя\ линия\ \mathrm{\Delta}DHC.\]

\[Обозначим:\ \]

\[HK = KC = a.\]

\[2)\ В\ \mathrm{\Delta}CEK:\]

\[EK = \sqrt{EC^{2} - KC^{2}} =\]

\[= \sqrt{3^{2} - a^{2}} = \sqrt{9 - a^{2}}.\]

\[3)\ Получаем:\]

\[\sqrt{9 - a^{2}} = (3 + a) \cdot tga\]

\[9 - a^{2} = (3 + a)^{2}tg^{2}a\]

\[9 - a^{2} = \left( 9 + 6a + a^{2} \right)tg^{2}a\]

\[a = \frac{- 6tg^{2}a \pm 6}{2\left( tg^{2}a + 1 \right)}\ (a > 0)\]

\[a = 3\frac{1 - tg^{2}a}{1 + tg^{2}a} =\]

\[= 3\frac{\frac{\cos^{2}{a - sin^{2}a}}{\cos^{2}a}}{\frac{\cos^{2}{a + \sin^{2}a}}{\cos^{2}a}} = 3cos2a.\]

\[EK = \sqrt{9 - a^{2}} =\]

\[= \sqrt{9 - 9\cos^{2}{2a}} = 3sin2a.\]

\[h = DH = 2EK = 6sin2a.\]

\[S = S_{\text{ADHB}} + S_{\text{DCN}} =\]

\[= h \cdot AD + \frac{1}{2}h \cdot HC =\]

\[= h\left( AD + \frac{\text{HC}}{2} \right) =\]

\[= 6sin2a(3 + 3cos2a) =\]

\[= 18sin2a( + cos2a).\]

\[Ответ:18 \cdot sin2a(1 + cos2a).\]