Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 1388
Задание 1388
\[\boxed{\mathbf{1388.еуроки - ответы\ на\ пятёрку}}\]
\[\textbf{а)}\ Дано:\]
\[точки\ A\ и\ B;\]
\[\ k > 0,\ k \neq 1;\]
\[\ AM = kBM.\]
\[Доказать:\ \]
\[\left\{ M \right\} - окружность.\]
\[Доказательство.\]
\[1)\ Пусть\ AB = a.\ \]
\[Выберем\ СК\ так,\ что\ A(0;0),\ \]
\[B(a;0),\ M(x;y).\]
\[2)\ Квадраты\ расстояний:\]
\[AM^{2} = x^{2} + y^{2};\ \ \]
\[BM^{2} = (x - a)^{2} + y^{2};\]
\[AM^{2} = k^{2} \cdot BM^{2}\text{.\ \ }\]
\[x^{2} + y^{2} = k^{2}\left( (x - a)^{2} + y^{2} \right)\]
\[x^{2} - k^{2}(x - a)^{2} + \left( 1 - k^{2} \right)y^{2} =\]
\[= 0\]
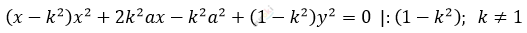
\[x^{2} + 2\frac{k^{2}a}{1 - k^{2}}x + y^{2} = \frac{k^{2}a^{2}}{1 - k^{2}}\]
\[x^{2} + 2\frac{k^{2}a}{1 - k^{2}}x + \left( \frac{k^{2}a}{1 - k^{2}} \right)^{2} + y^{2} =\]
\[= \frac{k^{2}a^{2}}{1 - k^{2}} + \left( \frac{k^{2}a}{1 - k^{2}} \right)^{2}\]
\[\frac{k^{2}a^{2}}{1 - k^{2}} + \left( \frac{k^{2}a}{1 - k^{2}} \right)^{2} =\]
\[= \frac{k^{2}a^{2}}{1 - k^{2}}\left( 1 + \frac{k^{2}}{1 - k^{2}} \right) =\]
\[= \frac{k^{2}a^{2}}{\left( 1 - k^{2} \right)^{2}}\]
\[\left( x + \frac{k^{2}a}{1 - k^{2}} \right)^{2} + y^{2} = \frac{k^{2}a^{2}}{\left( 1 - k^{2} \right)^{2}}\]
\[Это\ окружность\ с\ центром\ \]
\[C\left( - \frac{k^{2}a}{1 - k^{2}};0 \right)и\ \ радиусом\]
\[R = \frac{\text{ka}}{1 - k^{2}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ Дано:\]
\[O(C,R) - окружность\ \]
\[Аполлония\ O_{1}(D,\ r);\ \]
\[A \in O_{1};\ \]
\[B \in O_{1}.\]
\[Доказать:\]
\[радиусы\ взаимно\ \]
\[перпедикулярны\ в\ точке\ \]
\[E = O_{a} \cap O_{1}.\]
\[Доказательство.\]
\[1)\ В\ выбранной\ СК\ центр\ \]
\[окружности\ Аполлония\ \]
\[расположен\ на\ оси\ абсцисс.\]
\[2)\ Найдем\ центр\ окружности\]
\[\ O_{1};\ \ DA = r;\ DA^{2} = DB^{2}:\]
\[x^{2} + y^{2} = (x - a)^{2} + y^{2}\]
\[x^{2} + y^{2} = x^{2} - 2ax + a^{2} + y^{2}\]
\[x = \frac{a^{2}}{2a} = \frac{a}{2} - прямая,\ \]
\[параллельная\ Oy;\]
\[x_{D} = \frac{a}{2}.\]
\[3)\ Центр\ окружности\ O_{1}\ \]
\[расположен\ на\ серединном\ \]
\[перпедикуляре\ к\ отрезку\ \text{AB.}\]
\[4)\ Уравнение\ окружности:\]
\[\left( x - \frac{a}{2} \right)^{2} + \left( y - y_{D} \right)^{2} =\]
\[= \left( \frac{a}{2} \right)^{2} + y_{D}^{2}.\]
\[5)\ Расстояние\ между\ \]
\[центрами\ окружностей:\]
\[CD^{2} = \left( \frac{a}{2} + \frac{k^{2}a}{1 - k^{2}} \right)^{2} + y_{D}^{2} =\]
\[= \left( \frac{a}{2} \right)^{2} + \frac{k^{2}a^{2}}{1 - k^{2}} + \left( \frac{k^{2}a}{1 - k^{2}} \right)^{2} + y_{D}^{2} =\]
\[6)\ Квадраты\ расстояний\ \]
\[до\ точки\ пересечения\ \]
\[окружностей:\]
\[CE^{2} = R^{2} = \frac{k^{2}a^{2}}{\left( 1 - k^{2} \right)^{2}},\ \ \ \ \]
\[DE^{2} = r^{2} = \left( \frac{a}{2} \right)^{2} + y_{D}^{2}.\]
\[7)\ Сумма\ квадратов\ \]
\[расстояний:\]
\[CE^{2} + DE^{2} =\]
\[= \frac{k^{2}a^{2}}{\left( 1 - k^{2} \right)^{2}} + \left( \frac{a}{2} \right)^{2} + y_{D}^{2} = CD^{2}.\]
\[Значит:\]
\[\mathrm{\Delta}CED - прямоугольный\ \]
\[с\ \angle E = 90^{0}.\]
\[Что\ и\ требовалось\ доказать.\]
