Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 1370
Задание 1370
\[\boxed{\mathbf{1370.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
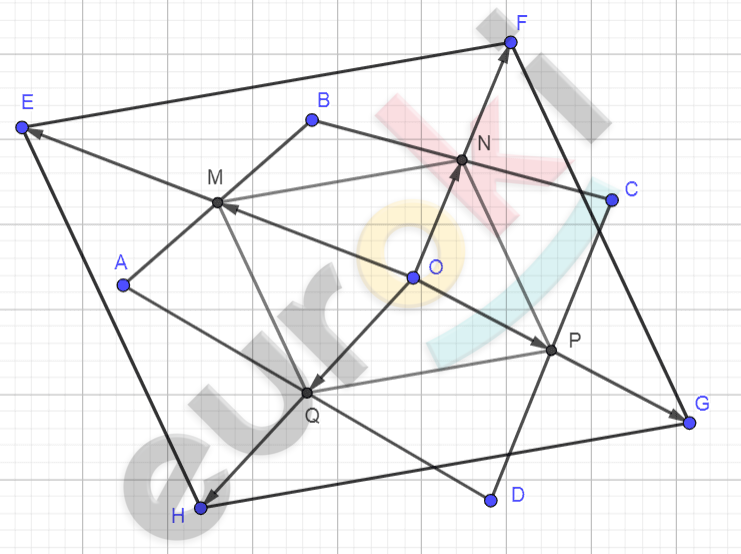
\[ABCD - четырехугольник;\]
\[M,N,P,Q - середины;\]
\[E,F,G,H - симметричны\ O\ \]
\[относительно\ M,N,P,Q.\]
\[\mathbf{Найти:}\]
\[Вид\ EFGH - ?\]
\[\mathbf{Решение.}\]
\[1)\ Определим\ вид\ \text{MNPQ.}\]
\[Пусть\ \overrightarrow{\text{AM}} = \overrightarrow{\text{MB}} = \overrightarrow{a},\]
\[\ \overrightarrow{\text{BN}} = \overrightarrow{\text{NC}} = \overrightarrow{b};\ \overrightarrow{\text{CP}} = \overrightarrow{\text{PD}} = \overrightarrow{c},\]
\[\overrightarrow{\text{DQ}} = \overrightarrow{\text{QA}} = \overrightarrow{d}:\]
\[\overrightarrow{\text{AB}} = \overrightarrow{\text{AD}} + \overrightarrow{\text{DC}} + \overrightarrow{\text{CB}}\ \]
\[2\overrightarrow{a} = - 2\overrightarrow{d} - 2\overrightarrow{c} - 2\overrightarrow{b}\]
\[\overrightarrow{a} + \overrightarrow{b} = - \left( \overrightarrow{c} + \overrightarrow{d} \right).\]
\[Отсюда:\ \ \]
\[\overrightarrow{\text{MN}} = - \overrightarrow{\text{QP}} = \overrightarrow{\text{PQ}};\]
\[MN \parallel QP\ и\ MN = QP.\]
\[Следовательно:\ \]
\[MNPQ - параллелограмм.\]
\[2)\ \overrightarrow{\text{OM}} = \overrightarrow{\text{ME}},\ \overrightarrow{\text{ON}} = \overrightarrow{\text{NF}},\]
\[\overrightarrow{\text{OP}} = \overrightarrow{\text{PG}},\overrightarrow{\text{OQ}} = \overrightarrow{\text{QH}}\ (так\ как\ \]
\[точки\ E,F,G,H\ симметрричны\ \]
\[точке\ \text{O\ }относительно\ точек\ \]
\[M,N,P,Q).\]
\[3)\ Рассмотрим\ треугольник\ \]
\[OEF:\]
\[MN - средня\ линия \Longrightarrow \ \]
\[\Longrightarrow EF = 2MN\ и\ MN \parallel EF.\]
\[4)\ Аналогично:\]
\[HG = 2QP\ и\ HG \parallel QP,\ \]
\[EH = 2MQ\ и\ EH \parallel MQ,\]
\[\ FG = 2NP\ и\ FG \parallel NP.\]
\[5)\ Следовательно:\ \]
\[HG = EF\ и\ HG \parallel EF,\ \]
\[EH = FG\ и\ EH \parallel FG.\]
\[Отсюда:\]
\[EFGH - параллелограмм,\ \]
\[каждая\ сторона\ которого\ \]
\[в\ два\ раза\ больше\ чем\ \]
\[у\ \text{MNPQ.}\]
\[\mathbf{Ответ:}EFGH -\]
\[параллелограмм.\]
