Решебник по геометрии 9 класс Атанасян ФГОС Вопросы для повторения к главе III

\[\boxed{Вопросы\ для\ повторения\ к\ глав\mathbf{е\ ІІІ.\ }\mathbf{еуроки - ответы\ на\ пятёрку}\mathbf{\ }}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Две\ прямые\ на\ плоскости\ }\]

\[\mathbf{называются\ параллельными,\ }\]

\[\mathbf{если\ они\ не\ пересекаются}\mathbf{.}\]

\[\mathbf{Два\ отрезка\ называются\ }\]

\[\mathbf{параллельными,\ если\ они\ }\]

\[\mathbf{лежат\ на\ параллельных\ }\]

\[\mathbf{прямых}\mathbf{.}\]

\[\boxed{\mathbf{2.}}\]

\[\mathbf{Прямая\ }\mathbf{\text{c\ }}\mathbf{называется\ секущей\ }\]

\[\mathbf{по\ отношению\ к\ прямым\ }\mathbf{\text{a\ }}\mathbf{и\ }\mathbf{b}\mathbf{,\ }\]

\[\mathbf{если}\mathbf{\ }\mathbf{она\ пересекает\ их\ в\ двух\ }\]

\[\mathbf{точках}\mathbf{.}\]

\[\mathbf{Пары\ углов,\ которые\ }\]

\[\mathbf{образовываются\ при\ }\]

\[\mathbf{пересечении\ двух}\]

\[\mathbf{параллельных\ прямых\ }\]

\[\mathbf{секущей:}\]

\[\mathbf{- накрест\ лежащие;}\]

\[\mathbf{- односторонние;}\]

\[\mathbf{- соответственные.}\]

\[\boxed{\mathbf{3.}}\]

\[Дано:\]

\[прямые\ a;b;\]

\[c - секущая;\]

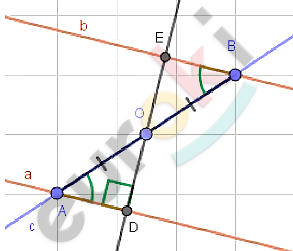
\[\angle EBA = \angle DAB.\]

\[Доказать:\]

\[a \parallel b.\]

\[Доказательство.\]

\[1)\ Отметим\ точку\ O - центр\ \]

\[отрезка\ AB:\]

\[AO = OB.\]

\[2)\ Опустим\ из\ \]

\[точки\ \text{O\ }\bot на\ прямую\ a:\]

\[OD\bot a.\]

\[3)\ Продолжим\ перпендикуляр.\]

\[E - точка\ пересечния\ \]

\[прямых\ \text{OD\ }и\ \text{b.}\]

\[4)\ ⊿AOD = ⊿BOE - по\ второму\ \]

\[признаку.\]

\[AO = OB;\]

\[\angle DAO = \angle EBO\ \]

\[(так\ как\ \angle DAB = \angle EBA);\]

\[\angle AOD = \angle BOE.\]

\[Из\ равенства\ треугольников:\]

\[\angle OEB = \angle ODA = 90{^\circ};\]

\[DE\bot b.\]

\[5)\ Получаем:\]

\[OD\bot a;\ \ DE\bot a;\ \ DE\bot B.\]

\[Отсда:\]

\[a \parallel b.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{4.}}\]

\[Дано:\]

\[a;b - прямые;\]

\[c - секущая;\]

\[\angle 1 = \angle 2.\]

\[Доказать:\]

\[a \parallel b.\]

\[Доказательство.\]

\[1)\ \angle 3\ и\ \angle 2 - вертикальные:\]

\[\angle 3 = \angle 2 = \angle 1.\]

\[2)\ \angle 1 = \angle 3 - накрест\ лежащие:\]

\[a \parallel b.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{5.}}\]

\[Дано:\]

\[a;b - прямые;\]

\[c - секущая;\]

\[\angle 1 + \text{∠}\text{2} = 180{^\circ}.\]

\[Доказать:\]

\[a \parallel b.\]

\[Доказательство.\]

\[1)\ \angle 3\ и\ \angle 2 - смежные:\]

\[\angle 3 = 180{^\circ} - \angle 2 = \angle 1.\]

\[2)\ \angle 1 = \angle 3 - накрест\ лежащие:\]

\[a \parallel b.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{6.}}\]

\[\mathbf{На\ практике\ параллельные\ }\]

\[\mathbf{прямые\ проводят\ с\ помощью\ }\]

\[\mathbf{чертежного\ треугольника\ и\ }\]

\[\mathbf{линейки;\ рейсшины\ }\]

\[\left( \mathbf{чертежные\ работы} \right)\mathbf{;}\mathbf{\ }\]

\[\mathbf{малки\ (столярные\ работы).}\]

\[\boxed{\mathbf{7.}}\]

\[\mathbf{Утверждения,\ которые\ }\]

\[\mathbf{принимаются\ в\ качестве\ }\]

\[\mathbf{исходных\ положений,\ }\]

\[\mathbf{на\ основе\ которых\ }\]

\[\mathbf{доказываются\ далее\ теоремы,\ }\]

\[\mathbf{называются\ аксиомами.}\mathbf{\ }\]

\[\mathbf{Пример\ аксиомы:}\]

\[\mathbf{через\ любые\ две\ точки\ }\]

\[\mathbf{проходит\ прямая\ и\ притом\ }\]

\[\mathbf{только\ одна.}\]

\[\boxed{\mathbf{8.}}\]

\[\mathbf{Доказательство.\ }\]

\[\mathbf{Согласно\ аксиоме\ }\]

\[\mathbf{параллельных\ прямых\ через\ }\]

\[\mathbf{точку,\ не\ лежащую\ на\ данной\ }\]

\[\mathbf{прямой,\ проходит\ только\ одна\ }\]

\[\mathbf{прямая,\ параллельная\ данной}\mathbf{.}\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{9.}}\]

\[\mathbf{Аксиома\ параллельных\ }\]

\[\mathbf{прямых:\ }\]

\[\mathbf{через\ точку,\ не\ лежащую\ }\]

\[\mathbf{на\ данной\ прямой,\ проходит\ }\]

\[\mathbf{только\ одна\ прямая,\ }\]

\[\mathbf{параллельная\ данной}\mathbf{.}\]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Утверждение,\ которое\ }\]

\[\mathbf{выводится\ непосредственно\ }\]

\[\mathbf{из\ аксиом\ или\ теорем,\ }\]

\[\mathbf{называется\ следствием}\mathbf{.}\]

\[Следствие\ из\ теоремы\ 1^{0}:\]

\[если\ прямая\ пересекает\ одну\ \]

\[из\ двух\ параллельных\ прямых,\ \]

\[то\ она\ пересекает\ и\ другую.\]

\[Пусть\ a \parallel b;\ \ прямая\ \text{c\ }\]

\[пересекает\ \text{a\ }в\ точке\ \text{M.}\]

\[Докажем,\ что\ прямая\ c\ \]

\[пересекает\ и\ \text{b.}\]

\[Если\ бы\ прямая\ c\ \]

\[не\ пересекала\ прямую\ b,\ \]

\[то\ через\ точку\ M\ проходило\ \]

\[бы\ две\ прямые,\ \]

\[параллельные\ b.\]

\[Но\ это\ противоречит\ аксимое\ \]

\[параллельных\ прямых:\]

\[значит,\ прямая\ c\ пересекает\ \]

\[прямую\ \text{b.}\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{11.}}\]

\[Следствие\ из\ теореме\ 2^{0}:\]

\[если\ две\ прямые\ параллельны\ \]

\[третьей,\ то\ они\ параллельны.\]

\[Пусть\ прямые\ a\ и\ \text{b\ }\]

\[параллельны\ прямой\ \text{c.}\]

\[Докажем,\ что\ a \parallel b.\]

\[Допустим,\ что\ прямые\ a\ и\ \text{b\ }\]

\[не\ параллельны,\ то\ есть\ \]

\[пересекаются\ в\ некоторой\ \]

\[точке\ M.\]

\[Тогда\ через\ точку\ M\ проходят\ \]

\[две\ прямые,\ параллельные\ \]

\[прямой\ \text{c.}\]

\[Но\ это\ противоречит\ аксиоме\ \]

\[параллельных\ прямых.\]

\[Наше\ предположение\ неверно,\ \]

\[следовательно:\]

\[a \parallel b.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Теоремой,\ обратной\ данной,\ }\]

\[\mathbf{называется\ такая\ теорема,\ }\]

\[\mathbf{в\ которой\ условием\ является\ }\]

\[\mathbf{заключение\ данной\ теоремы,\ }\]

\[\mathbf{а\ заключением\ -}\mathbf{\ }\mathbf{условие\ }\]

\[\mathbf{данной\ теоремы}\mathbf{.}\]

\[\mathbf{Пример:\ }\]

\[\mathbf{Если\ две\ параллельные\ }\]

\[\mathbf{прямые\ пересечены\ секущей,\ }\]

\[\mathbf{то\ накрест\ лежащие\ углы\ }\]

\[\mathbf{равны}\mathbf{.}\]

\[\mathbf{Обратная\ теорема:\ }\]

\[\mathbf{Если\ при\ пересечении\ двух\ }\]

\[\mathbf{прямых\ секущей\ накрест\ }\]

\[\mathbf{лежащие\ углы\ равны,\ }\]

\[\mathbf{то\ прямые\ параллельны}\mathbf{.}\]

\[\boxed{\mathbf{13.}}\]

\[Дано:\]

\[a \parallel b;\]

\[MN - секущая.\]

\[Доказать:\]

\[\angle 1 = \angle 2.\]

\[Доказательство.\]

\[Допустим,\ что\ углы\ 1\ и\ 2\ \]

\[не\ равны.\]

\[Построим\ \angle PMN = \angle 2\ так,\ \]

\[чтобы\ эти\ углы\ были\ накрест\ \]

\[лежащими.\]

\[\angle PMN = 2 - по\ построению:\]

\[MP \parallel b.\]

\[Получили,\ что\ через\ точку\ \text{M\ }\]

\[проходит\ две\ прямые\ \parallel b:\]

\[a \parallel b;\ \ \ MP \parallel b;\ \ M \in a.\]

\[Но\ это\ противоречит\ условию\ \]

\[параллельности\ прямых.\]

\[Значит,\ наше\ допущение\ \]

\[неверно:\]

\[\angle 1 = \angle 2.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{14.}}\]

\[Дано:\]

\[a \parallel b;\]

\[MN\bot a.\]

\[Доказать:\]

\[MN\bot b.\]

\[Доказательство.\]

\[MN\bot a:\]

\[\angle 1 = 90{^\circ}.\]

\[MN - секущая.\]

\[При\ пересечении\ секущей\ \]

\[пары\ параллельных\ прямых,\ \]

\[накрест\ лежащие\ углы\ равны:\]

\[\angle 2 = \angle 1 = 90{^\circ}.\]

\[Следовательно:\]

\[MN\bot b.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{15.}}\]

\[Дано:\]

\[a \parallel b;\]

\[MN - секущая.\]

\[Доказать:\]

\[\textbf{а)}\ \angle 1 = \angle 3;\]

\[\textbf{б)}\ \angle 1 + \angle 4 = 180{^\circ}.\]

\[Доказательство.\]

\[\textbf{а)}\ a \parallel b;\ \ MN - секущая:\]

\[\angle 1 = \angle 2 - как\ накрест\ \]

\[лежащие.\]

\[\angle 3 = \angle 2 - как\ вертикальные.\]

\[Отсюда:\]

\[\angle 1 = \angle 3.\]

\[\textbf{б)}\ a \parallel b;\ \ MN - секущая:\]

\[\angle 1 = \angle 2 - как\ накрест\ \]

\[лежащие.\]

\[\angle 2 + \angle 4 = 180{^\circ} - как\ смежные.\]

\[Отсюда:\]

\[\angle 1 + \angle 4 = 180{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{16.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{если\ стороны\ одного\ угла\ }\]

\[\mathbf{соответственно\ параллельны\ }\]

\[\mathbf{сторонам\ другого\ угла,\ }\]

\[\mathbf{то\ такие\ углы\ или\ равны,\ }\]

\[\mathbf{или\ в\ сумме\ составляют\ }180{^\circ}.\]

\[Дано:\]

\[\angle\text{AOB\ }и\ \angle A_{1}O_{1}B_{1};\]

\[OA \parallel O_{1}A_{1};\]

\[OB \parallel O_{1}B_{1}.\]

\[Доказать:\]

\[\angle AOB = \angle A_{1}O_{1}B_{1};\]

\[\angle AOB + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[Доказательство.\]

\[Если\ угол\ AOB - развернутый,\ \]

\[значит\ лучи\ OA\ \ и\ OB\ будут\ \]

\[лежать\ на\ одной\ прямой,\ \]

\[при\ этом\ по\ условию\ OA \parallel O_{1}A_{1},\ \]

\[OB \parallel O_{1}B_{1}.\]

\[Значит,\ точки\ O_{1}A_{1}\ \ и\ O_{1}B_{1}\text{\ \ }\]

\[также\ будут\ лежать\ на\ одной\ \]

\[прямой.\]

\[Следовательно,\angle A_{1}O_{1}B_{1} - \ \]

\[будет\ развернутым,\ тогда\ \ \]

\[\angle AOB = \angle A_{1}O_{1}B_{1}.\]

\[Если\ угол\ AOB -\]

\[не\ развернутый,\ то\ возможны\ \]

\[два\ случая\ расположения\]

\[углов\ \text{AOB\ }и\ A_{1}O_{1}B_{1}.\]

\[Случай\ 1.\]

\[Прямая\ O_{1}B_{1}\ пересекает\ O_{1}A_{1}\ и,\ \]

\[следовательно,\ пересекает\ \]

\[параллельную\ ей\ прямую\ OA\ \]

\[в\ некоторой\ точке\ \text{M\ }\]

\[(следствие\ из\ аксиомы\ \]

\[параллельных\ прямых).\]

\[OB \parallel O_{1}B_{1}\ пересечены\ \]

\[секущей\ \text{OM},\ поэтому\ \angle 1,\ \]

\[образованный\ при\ \]

\[пересечении\ прямых\ O_{1}B_{1}\ и\ \text{OA},\ \]

\[равен\ \angle AOB:\]

\[\angle 1 = \angle AOB - по\ теореме\ \]

\[о\ накрест\ лежащих\ углах.\]

\[OA \parallel O_{1}A_{1};\ \ O_{1}M - секущая:\]

\[\angle 1 = \angle A_{1}O_{1}B_{1}.\]

\[Отсюда:\]

\[\angle AOB = \angle A_{1}O_{1}B_{1}.\]

\[Случай\ 2.\]

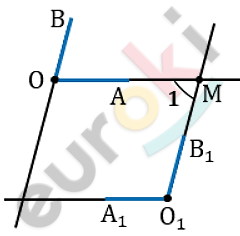
\[Прямая\ O_{1}B_{1}\ пересекает\ O_{1}A_{1}\ и,\ \]

\[следовательно,\ пересекает\ \]

\[параллельную\ ей\ прямую\ OA\ \]

\[в\ некоторой\ точке\ \text{M\ }\]

\[(следствие\ из\ аксиомы\ \]

\[параллельных\ прямых).\]

\[OB \parallel O_{1}B_{1}\ пересечены\ \]

\[секущей\ \text{OM},\ поэтому\ \angle 1,\ \]

\[образованный\ при\]

\[пересечении\ прямых\ O_{1}B_{1}\ \]

\[и\ \text{OA},\ равен\ \angle AOB:\]

\[\angle 1 + \angle A_{1}O_{1}B_{1} = 180{^\circ} - по\ \]

\[теореме\ об\ односторонних\ \]

\[углах.\]

\[OA \parallel O_{1}A_{1};\ \ O_{1}M - секущая:\]

\[\angle 1 = \angle A_{1}O_{1}B_{1}.\]

\[Отсюда:\]

\[\angle AOB + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{Теорема.}\]

\[\mathbf{Если\ стороны\ одного\ угла\ }\]

\[\mathbf{соответственно\ }\]

\[\mathbf{перпендикулярны\ сторонам\ }\]

\[\mathbf{другого\ угла,\ то\ такие\ углы\ }\]

\[\mathbf{или\ равны,\ или\ в\ сумме}\mathbf{\ }\]

\[составляют\ 180{^\circ}.\]

\[Доказательство.\]

\[Если\ \angle AOB = 180{^\circ},\ то\ обе\ его\ \]

\[стороны\ лежат\ на\ одной\ \]

\[прямой.\]

\[Соответственные\ \]

\[перпендикулярные\ стороны\ \]

\[\angle A_{1}O_{1}B_{1}\ тоже\ лежат\]

\[на\ одной\ прямой,\ \bot первой.\]

\[Значит:\ \ \]

\[\angle A_{1}O_{1}B_{1} = \angle AOB = 180{^\circ}.\]

\[Если\ \angle AOB = 90{^\circ},\ то\ обе\ его\ \]

\[стороны\ перпендикулярны.\]

\[Соответственные\ \]

\[перпендикулярные\ стороны\ \]

\[\angle A_{1}O_{1}B_{1}\ будут\ \parallel сторонам\ \]

\[\angle\text{AOB}:\]

\[\angle A_{1}O_{1}B_{1} = \angle AOB = 90{^\circ}.\]

\[Случай\ 1.\]

\[\angle AOB < 90{^\circ} - острый.\]

\[Проведем\ OC\bot OA;\ \ OD\bot OB.\]

\[Точки\ C\ и\ \text{D\ }лежат\ с\ \text{B\ }\]

\[в\ противоположных\ \]

\[плоскостях\ относительно\]

\[прямой\ \text{OA.}\]

\[OC\bot OA;OA\bot O_{1}A_{1}:\]

\[OC \parallel O_{1}A_{1}.\]

\[OD\bot OB;\ \ OB\bot O_{1}B_{1}:\]

\[OD \parallel O_{1}B_{1}.\]

\[Так\ как\ стороны\ уголов\ COD\ \]

\[и\ A_{1}O_{1}B_{1}\ попарно\ \parallel :\]

\[\angle COD = \angle A_{1}O_{1}B_{1}\ или\ \]

\[\angle COD + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[\angle AOB = \angle BOD - \angle AOD;\ \ \]

\[\angle BOD = 90{^\circ}:\]

\[\angle AOB = 90{^\circ} - \angle AOD.\]

\[\angle COD = \angle AOC - \angle AOD;\ \ \]

\[\angle AOC = 90{^\circ}:\]

\[\angle COD = 90{^\circ} - \angle AOD.\]

\[Отсюда:\]

\[\angle AOB = \angle COD.\]

\[Следовательно:\]

\[\angle AOB = \angle A_{1}O_{1}B_{1};\ \ или\]

\[\angle AOB + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[Случай\ 2.\]

\[90{^\circ} < \angle AOB < 180{^\circ} - тупой.\]

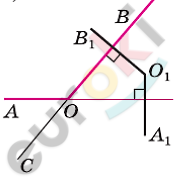
\[Проведем\ луч\ OC -\]

\[дополнительный\ к\ лучу\ \text{OB.}\]

\[Получим\ острый\ \angle AOC:\]

\[OA\bot O_{1}A_{1};\]

\[OC\bot O_{1}B_{1}.\]

\[Получаем\ случай\ 1\ (см.\ выше):\ \]

\[\angle AOB = \angle A_{1}O_{1}B_{1};\ \ или\]

\[\angle AOB + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[\angle AOC\ и\ \angle AOB - сопряженные:\]

\[\angle AOC = 180{^\circ} - \angle AOB.\]

\[Отсюда:\]

\[1)\ 180{^\circ} - \angle AOB = \angle A_{1}O_{1}B_{1}\]

\[\angle AOB + \angle A_{1}O_{1}B_{1} = 180{^\circ}.\]

\[или\]

\[2)\ 180{^\circ} - \angle AOB + \angle A_{1}O_{1}B_{1} =\]

\[= 180{^\circ}\]

\[\angle AOB = \angle A_{1}O_{1}B_{1}.\]

\[Что\ и\ требовалось\ доказать.\]