Решебник по геометрии 9 класс Атанасян ФГОС Вопросы для повторения к главе II

\[\boxed{Вопросы\ для\ повторения\ к\ глав\mathbf{е\ ІІ.\ }\mathbf{еуроки - ответы\ на\ пятёрку}\mathbf{\ }}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Треугольник - это\ }\]

\[\mathbf{геометрическая\ фигура,\ }\]

\[\mathbf{образованная\ тремя\ отрезками,\ }\]

\[\mathbf{которые\ соединяют\ три\ }\]

\[\mathbf{не\ лежащие\ на\ одной\ прямо}\mathbf{й}\]

\[\mathbf{точки.}\]

\[\mathbf{Периметр\ треугольника - это\ }\]

\[\mathbf{сумма\ длин\ трех\ его\ сторон.}\]

\[Отрезки\ AB;BC;AC - стороны.\]

\[Точки\ A;B;C - вершины.\]

\[\angle A;\ \angle B;\ \angle C - углы.\]

\[\boxed{\mathbf{2.}}\]

\[\mathbf{Два\ треугольника\ называют\ }\]

\[\mathbf{равными,\ если\ их\ можно\ }\]

\[\mathbf{совместить}\mathbf{\ }\mathbf{наложением}\mathbf{.}\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Теорема - это\ утверждение,\ }\]

\[\mathbf{справедливость\ которого\ }\]

\[\mathbf{устанавливается}\mathbf{\ }\mathbf{путем\ }\]

\[\mathbf{рассуждений}\mathbf{.}\]

\[\mathbf{Доказательство\ теоремы -}\]

\[\mathbf{последовательность\ }\]

\[\mathbf{рассуждений,\ }\]

\[\mathbf{устанавливающих\ }\]

\[\mathbf{справедливость\ теоремы}\mathbf{.}\]

\[\boxed{\mathbf{4.}}\]

\[\mathbf{Первый\ признак\ равенства\ }\]

\[\mathbf{треугольников:}\]

\[\mathbf{если\ две\ стороны\ и\ угол\ между\ }\]

\[\mathbf{ними\ одного\ треугольника}\]

\[\mathbf{соответственно\ равны\ двум\ }\]

\[\mathbf{сторонам\ и\ углу\ между\ ними\ }\]

\[\mathbf{другого\ треугольника,\ то\ такие\ }\]

\[\mathbf{треугольники\ равны.}\]

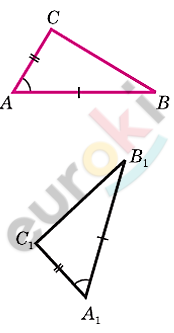
\[\mathbf{Дано:}\]

\[⊿ABC;\ ⊿A_{1}B_{1}C_{1};\]

\[AB = A_{1}B_{1};\]

\[AC = A_{1}C_{1};\]

\[\angle A = \angle A_{1}.\]

\[Доказать:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

\[Доказательство.\]

\[1)\ \angle A = \angle A_{1}:\]

\[⊿ABC\ можно\ наложить\ на\ \]

\[⊿A_{1}B_{1}C_{1}\ так,\ что\ вершина\ \text{A\ }\]

\[совместится\ с\ вершиной\ A_{1};\]

\[стороны\ AB\ и\ \text{AC\ }наложатся\ \]

\[на\ лучи\ A_{1}B_{1}\ и\ A_{1}C_{1}\ \]

\[соответственно.\]

\[2)\ AB = A_{1}B_{1}:\]

\[сторона\ AB\ совместится\ \]

\[со\ стороной\ A_{1}B_{1}.\]

\[AC = A_{1}C_{1}:\]

\[сторона\ AC\ совместится\ \]

\[со\ стороной\ A_{1}C_{1}.\]

\[Отсюда\ (в\ частности):\]

\[совместятся\ точки\ B\ и\ B_{1};\]

\[\text{C\ }и\ C_{1}.\]

\[3)\ Следовательно:\]

\[совместятся\ стороны\ \text{BC\ }и\ \]

\[B_{1}C_{1}.\]

\[Треугольники\ ABC\ и\ A_{1}B_{1}C_{1}\ \]

\[полностью\ совместятся:\]

\[значит,\ они\ равны.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Отрезок\ называется\ }\]

\[\mathbf{перпендикуляром,\ }\]

\[\mathbf{проведенным\ из\ данной\ точки}\]

\[\mathbf{к\ прямой,\ если\ прямые\ }\]

\[\mathbf{перпендикулярны.}\]

\[\boxed{\mathbf{6.}}\]

\[\mathbf{Теорема\ о\ перпендикуляре:}\]

\[\mathbf{из\ точки,\ не\ лежащей\ }\]

\[\mathbf{на\ прямой,\ можно\ провести\ }\]

\[\mathbf{перпендикуляр\ к\ этой\ прямой,\ }\]

\[\mathbf{и\ притом\ только\ один}\mathbf{.}\]

\[Дано:\]

\[BC - прямая;\]

\[точка\ A \notin BC.\]

\[Доказать:\]

\[1)\ через\ точку\ \text{A\ }можно\ \]

\[провести\ \bot BC;\]

\[2)\ перпендикуляр\ \]

\[единственный.\]

\[Доказательство.\]

\[1)\ Отложим\ от\ луча\ \text{BC\ }углы:\ \]

\[\angle MBC = \angle ABC.\]

\[2)\ Наложим\ \angle MBC\ на\ \angle ABC:\]

\[\text{BC\ }и\ BA - совместятся\ с\ \text{BC\ }и\ \]

\[\text{BM};\]

\[точка\ \text{A\ }наложится\ \]

\[на\ точку\ A_{1} \in BM.\]

\[3)\ H - точка\ пересечения\ AA_{1}\ \]

\[и\ \text{BC.}\]

\[4)\ AH\bot BC.\]

\[Допустим,\ что\ существует\ \]

\[другой\ перпендикуляр\ AH_{1}:\]

\[AH\bot BC\ и\ AH_{1}\bot BC - но\ это\ \]

\[невозможно.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{7.}}\]

\[\mathbf{Медиана\ треугольника - это\ }\]

\[\mathbf{отрезок,\ соединяющий\ }\]

\[\mathbf{вершину\ с\ серединой\ }\]

\[\mathbf{противоположной\ стороны}\mathbf{.}\]

\[\mathbf{Любой\ треугольник\ имеет\ }\]

\[\mathbf{три\ медианы,\ которые\ }\]

\[\mathbf{пересекаются}\mathbf{\ }\mathbf{в\ одной\ точке}\mathbf{.}\]

\[\boxed{\mathbf{8.}}\]

\[\mathbf{Биссектриса\ треугольника -}\]

\[\mathbf{это\ отрезок\ биссектрисы\ угла,\ }\]

\[\mathbf{соединяющий\ вершину\ }\]

\[\mathbf{с\ точкой\ на\ противоположной\ }\]

\[\mathbf{стороне}\mathbf{\ }\mathbf{треугольника}\mathbf{.}\]

\[\mathbf{Любой\ треугольник\ имеет\ }\]

\[\mathbf{три\ биссектрисы,\ }\]

\[\mathbf{пересекающиеся\ в\ одной\ точке}\mathbf{.}\]

\[\boxed{\mathbf{9.}}\]

\[\mathbf{Высота\ треугольника - это\ }\]

\[\mathbf{перпендикуляр,\ проведенный\ }\]

\[\mathbf{из\ вершины}\mathbf{\ }\mathbf{к\ прямой,\ }\]

\[\mathbf{содержащей\ }\]

\[\mathbf{противоположную\ сторону}\mathbf{.}\]

\[\mathbf{Любой\ треугольник\ имеет\ }\]

\[\mathbf{три\ высоты.}\]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Треугольник\ называется\ }\]

\[\mathbf{равнобедренным,\ если\ две\ его\ }\]

\[\mathbf{стороны\ равны.Равные\ }\]

\[\mathbf{стороны\ называются\ }\]

\[\mathbf{боковыми\ сторонами}\mathbf{;}\]

\[\mathbf{третья\ сторона - основанием\ }\]

\[\mathbf{равнобедренного\ }\]

\[\mathbf{треугольника.}\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Равносторонний\ }\]

\[\mathbf{треугольник - это\ }\]

\[\mathbf{треугольник,\ у\ которого\ все\ }\]

\[\mathbf{три}\mathbf{\ }\mathbf{стороны\ равны}\mathbf{.}\]

\[\mathbf{Углы\ равностороннего\ }\]

\[\mathbf{треугольника\ также\ равны.}\]

\[\boxed{\mathbf{12.}}\]

\[Дано:\]

\[⊿ABC;\]

\[AB = AC.\]

\[Доказать:\]

\[\angle B = \angle C.\]

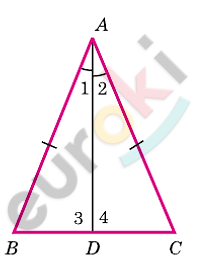
\[Доказательство.\]

\[1)\ Проведем\ AD - биссектрису\ \]

\[угла\ A:\]

\[D - точка\ пересечения\ \text{AD\ }и\ \text{BC.}\]

\[2)\ ⊿ABD = ⊿ACD -\]

\[по\ первому\ признаку:\]

\[AB = AC - по\ условию;\]

\[AD - общая\ сторона;\]

\[\angle BAD = CAD = \frac{1}{2}\angle A\ \]

\[(так\ как\ AD - биссектриса).\]

\[3)\ Из\ равенства\ треугольников\ \]

\[следует:\angle B = \angle C.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{13.}}\]

\[\mathbf{Теорема\ о\ биссектрисе\ }\]

\[\mathbf{равнобедренного\ }\]

\[\mathbf{треугольника:}\]

\[\mathbf{в\ равнобедренном\ }\]

\[\mathbf{треугольнике\ биссектриса,\ }\]

\[\mathbf{проведенная\ к\ основанию,\ }\]

\[\mathbf{является\ медианой\ и\ высотой}\mathbf{.}\]

\[\mathbf{Дано:}\]

\[⊿ABC;\]

\[AB = AC;\]

\[AD - биссектриса.\]

\[Доказать:\]

\[AD - медиана\ и\ высота.\]

\[Доказательство.\]

\[1)\ ⊿ABD = ⊿ACD - по\ первому\ \]

\[признаку:\]

\[AB = AC - по\ условию;\]

\[AD - общая\ сторона;\]

\[\angle BAD = CAD = \frac{1}{2}\angle A\ \]

\[(так\ как\ AD - биссектриса).\]

\[3)\ Из\ равенства\ треугольников\ \]

\[следует:\]

\[BD = DC \rightarrow AD - медиана.\]

\[\angle ADB = \angle ADC = \frac{1}{2}\angle BDC =\]

\[= \frac{1}{2} \cdot 180{^\circ} = 90{^\circ}:\]

\[AD - высота.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{14.}}\]

\[\mathbf{Второй\ признак\ равенства\ }\]

\[\mathbf{треугольников:если\ сторона\ }\]

\[\mathbf{и\ два\ прилежащих\ к\ ней\ угла\ }\]

\[\mathbf{одного\ треугольник}\mathbf{а}\]

\[\mathbf{соответственно\ равны\ стороне\ }\]

\[\mathbf{и\ двум\ прилежащим\ к\ ней\ }\]

\[\mathbf{углам}\mathbf{\ }\mathbf{другого\ треугольника,\ }\]

\[\mathbf{то\ такие\ треугольники\ равны}\mathbf{.}\]

\[\mathbf{Дано:}\]

\[⊿ABC;\ ⊿A_{1}B_{1}C_{1};\]

\[AB = A_{1}B_{1};\]

\[\angle A = \angle A_{1};\]

\[\angle B = \angle B_{1}.\]

\[Доказать:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

\[Доказательство.\]

\[1)\ Наложим\ ⊿ABC\ на\ ⊿A_{1}B_{1}C_{1}\ \]

\[так,\ чтобы:\]

\[вершина\ \text{A\ }совместилась\ \]

\[с\ вершиной\ A_{1};\]

\[сторона\ AB - с\ равной\ ей\ \]

\[стороной\ A_{1}B_{1};\]

\[вершины\ C\ и\ C_{1} - оказались\ \]

\[по\ одну\ сторону\ \]

\[от\ прямой\ A_{1}B_{1}.\]

\[2)\ \angle A = \angle A_{1};\ \ \angle B = \angle B_{1}:\]

\[сторона\ AC\ наложится\ \]

\[на\ луч\ A_{1}C_{1};\]

\[сторона\ BC - на\ луч\ B_{1}C_{1}.\]

\[Значит:\]

\[окажется\ лежащей\ как\ на\]

\[луче\ A_{1}C_{1},\ так\ и\ на\ луче\ B_{1}C_{1}.\]

\[Следовательно,\ точка\ C\ \]

\[совместится\ с\ общей\ точкой\ \]

\[лучей\ C_{1}.\]

\[3)\ Значит:\]

\[стороны\ AC\ и\ A_{1}C_{1};BC\ и\ \]

\[B_{1}C_{1} - совместятся.\]

\[Получаем:\]

\[⊿ABC\ и\ ⊿A_{1}B_{1}C_{1} - совместятся\ \]

\[полностью;\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

\[Теорема\ доказана.\ \]

\[\boxed{\mathbf{15.}}\]

\[\mathbf{Третий\ признак\ равенства\ }\]

\[\mathbf{треугольников:}\]

\[\mathbf{если\ три\ стороны\ одного\ }\]

\[\mathbf{треугольника\ соответственно\ }\]

\[\mathbf{равны\ трем}\mathbf{\ }\mathbf{сторонам\ другого\ }\]

\[\mathbf{треугольника,\ то\ такие\ }\]

\[\mathbf{треугольники\ равны}\mathbf{.}\]

\[Дано:\]

\[⊿ABC;\ ⊿A_{1}B_{1}C_{1};\]

\[AB = A_{1}B_{1};\ \]

\[BC = B_{1}C_{1};\]

\[AC = A_{1}C_{1}.\]

\[Доказать:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

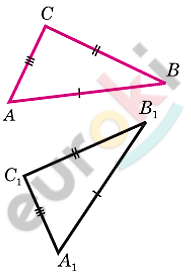
\[Доказательство.\]

\[1)\ Приложим\ ⊿\text{ABC\ }к\ ⊿A_{1}B_{1}C_{1}\ \]

\[так,\ чтобы\ вершина\ \text{A\ }\]

\[совместилась\ с\ вершиной\ A_{1};\]

\[вершина\ \text{B\ }с\ B_{1};вершины\ \text{C\ }и\ C_{1}\ \]

\[лежали\ по\ разные\ стороны\ \]

\[от\ прямой\ A_{1}B_{1}.\]

\[2)\ AC = A_{1}C_{1};BC = B_{1}C_{1} -\]

\[по\ аксиоме\ откладывания\ \]

\[отрезков:\]

\[⊿A_{1}C_{1}C\ и\ ⊿B_{1}C_{1}C -\]

\[равнобедренные.\]

\[3)\ По\ свойству\ \]

\[равнобедренного\ \]

\[треугольника:\]

\[\angle A_{1}C_{1}C = \angle A_{1}CC_{1};\ \ \]

\[\angle B_{1}C_{1}C = \angle B_{1}CC_{1}.\]

\[Отсюда:\]

\[\angle A_{1}CB_{1} = \angle A_{1}C_{1}B_{1}.\]

\[4)\ ⊿ABC = ⊿A_{1}B_{1}C_{1} -\]

\[по\ первому\ признаку:\]

\[AC = A_{1}C_{1};\]

\[BC = B_{1}C_{1};\]

\[\angle C = \angle C_{1}.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{16.}}\]

\[\mathbf{Определение - это\ }\]

\[\mathbf{предложение,\ в\ котором\ }\]

\[\mathbf{разъясняется\ смысл\ того\ или\ }\]

\[\mathbf{иного\ выражения\ или\ }\]

\[\mathbf{названия}\mathbf{.}\]

\[\mathbf{Окружность - это\ }\]

\[\mathbf{геометрическая\ фигура,\ }\]

\[\mathbf{состоящая\ из\ всех\ точек}\]

\[\mathbf{плоскости,\ расположенных\ на\ }\]

\[\mathbf{заданном\ расстоянии\ }\]

\[\mathbf{от\ данной\ точки.}\]

\[\mathbf{Данная\ точка\ называется\ }\]

\[\mathbf{центром\ окружности.}\]

\[\mathbf{Радиус - это\ отрезок,\ }\]

\[\mathbf{соединяющий\ центр\ и\ какую -}\]

\[\mathbf{либо\ точку}\mathbf{\ }\mathbf{на\ окружности}\mathbf{.}\]

\[\mathbf{Хорда - это\ отрезок,\ }\]

\[\mathbf{соединяющий\ две\ точки\ }\]

\[\mathbf{окружности.}\]

\[\mathbf{Диаметр - это\ хорда,\ }\]

\[\mathbf{проходящая\ через\ центр\ }\]

\[\mathbf{окружности.}\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{При\ помощи\ циркуля\ измерить\ }\]

\[\mathbf{отрезок.}\]

\[\mathbf{Потом\ нужно\ поставить\ ножку\ }\]

\[\mathbf{циркуля\ в\ начало\ луча\ и\ }\]

\[\mathbf{описать\ окружность\ }\]

\[\mathbf{с\ радиусом,\ равным\ отрезку}\mathbf{.}\]

\[\mathbf{Точка\ пересечения\ }\]

\[\mathbf{окружности\ и\ луча\ и\ есть\ }\]

\[\mathbf{второй\ конец\ отрезка,\ }\]

\[\mathbf{равного\ данному.}\]

\[OD - искомый\ отрезок.\]

\[\boxed{\mathbf{18.}}\]

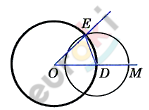
\[Дан\ угол\ с\ вершиной\ A\ и\ \]

\[луч\ OM.\ \]

\[Проведем\ окружность\ \]

\[произвольного\ радиуса\ \]

\[с\ центром\ в\ вершине\ A\ \]

\[данного\ угла.\ \]

\[Эта\ окружность\ пересекает\ \]

\[стороны\ угла\ в\ точках\ B\ и\ C.\ \]

\[Затем\ проведем\ окружность\ \]

\[того\ же\ радиуса\ с\ центром\ \]

\[в\ начале\ данного\ луча\ OM.\ \]

\[Эта\ окружность\ пересекает\ луч\ \]

\[в\ точке\ D.\ \]

\[После\ этого\ построим\ \]

\[окружность\ с\ центром\ D,\ \]

\[радиус\ которой\ равен\ BC.\ \]

\[Окружности\ с\ центрами\ O\ и\ D\ \]

\[пересекаются\ в\ двух\ точках.\ \]

\[Одну\ из\ этих\ точек\ обозначим\ \]

\[буквой\ E.\ \]

\[Угол\ MOE\ - \ искомый.\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Построение\ биссектрисы\ угла:}\]

\[1)\ построить\ окружность\ \]

\[произвольного\ радиуса\ \]

\[с\ центром\ в\ вершине\ угла\ и\ \]

\[отметить\ точки\ пересечения\ \]

\[этой\ окружности\ со\ сторонами\ \]

\[угла;\]

\[2)\ построить\ две\ окружности\ \]

\[с\ тем\ же\ радиусом,\ \]

\[но\ с\ центрами\ в\ полученных\ \]

\[точках\ на\ сторонах\ угла\ и\ \]

\[отметить\ точку\ их\ \]

\[пересечения;\]

\[3)\ из\ вершины\ \mathbf{угла\ через\ }\]

\[\mathbf{полученную\ точку\ построить\ }\]

\[\mathbf{луч.\ }\]

\[\mathbf{Этот\ луч\ и\ будет\ биссектрисой\ }\]

\[\mathbf{угла.}\]

\[\boxed{\mathbf{20.}}\]

\[Дана\ прямая\ a\ и\ дана\ точка\ M,\ \]

\[принадлежащая\ этой\ прямой.\ \]

\[На\ лучах\ прямой\ a,\ исходящих\ \]

\[из\ точки\ M,\ отложим\ равные\ \]

\[отрезки\ MA\ и\ MB.\ \]

\[Затем\ построим\ две\ \]

\[окружности\ с\ центрами\ A\ и\ B\ \]

\[радиуса\ AB.\ \]

\[Они\ пересекутся\ в\ двух\ точках:\ \]

\[P\ и\ Q.\ \]

\[Проведем\ прямую\ через\ \]

\[точку\ M\ и\ одну\ из\ этих\ точек:\ \]

\[например,\ прямую\ MP.\]

\[Эта\ прямая\ - \ искомая,\ то\ есть\ \]

\[она\ перпендикулярна\ к\ данной\ \]

\[прямой\ a.\]

\[\boxed{\mathbf{21.}}\]

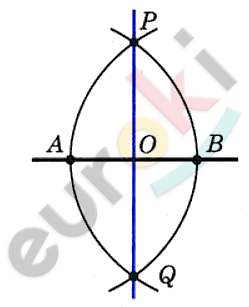
\[Пусть\ AB\ данный\ отрезок.\ \]

\[Построим\ две\ окружности\ \]

\[с\ центрами\ A\ и\ B\ радиуса\ AB.\ \]

\[Они\ пересекутся\ в\ точках\ \]

\[P\ и\ Q.\ Проведем\ прямую\ PQ.\ \]

\[Точка\ O\ пересечения\ этой\ \]

\[прямой\ с\ отрезком\ AB\ и\ \]

\[есть\ искомая\ середина\ \]

\[отрезка\ AB.\]