Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 904
Задание 904
\[\boxed{\mathbf{904.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[MNPQ - четырехугольник;\]
\[\overrightarrow{\text{ON}} - \overrightarrow{\text{OM}} = \overrightarrow{\text{OP}} - \overrightarrow{\text{OQ}}.\]
\[\mathbf{Найти:}\]
\[Вид\ MNPQ - ?\]
\[\mathbf{Решение.}\]
\[1)\ Найдем\ разности\ векторов:\]
\[\overrightarrow{\text{ON}} - \overrightarrow{\text{OM}} = \overrightarrow{\text{ON}} + \overrightarrow{\text{MO}} =\]
\[= \overrightarrow{\text{MO}} + \overrightarrow{\text{ON}} = \overrightarrow{\text{MN}};\]
\[\overrightarrow{\text{OP}} - \overrightarrow{\text{OQ}} = \overrightarrow{\text{OP}} + \overrightarrow{\text{QO}} =\]
\[= \overrightarrow{\text{QO}} + \overrightarrow{\text{OP}} = \overrightarrow{\text{QP}}.\]
\[2)\ \overrightarrow{\text{MN}} = \overrightarrow{\text{QP}} \Longrightarrow MN \parallel QP\ и\ \]
\[MN = QP:\]
\[MNPQ - параллелограмм\ \]
\[(по\ определению\ параллелограмма).\]
\[\mathbf{Ответ:}\]
\[MNPQ - параллелограмм.\]
\[\boxed{\mathbf{904.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[Окружность\ (O;R);\]
\[OA = R;\]
\[BD - касатель;\]
\[OB\bot BD;\]
\[AD\bot BD.\]
\[\mathbf{Доказать:}\]
\[\frac{AB^{2}}{\text{AD}} = const.\]
\[\mathbf{Доказательство.}\]
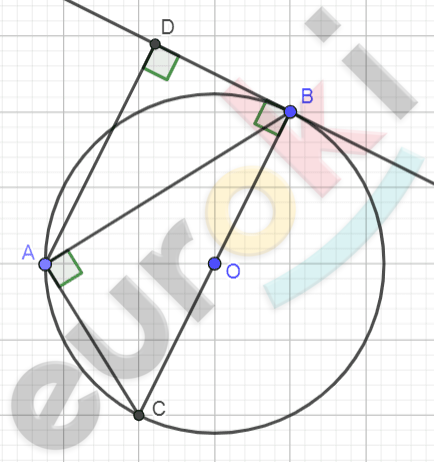
\[1)\ Пусть\ \text{A\ }не\ лежит\ \]
\[на\ диаметре,\ проведем\ \]
\[диаметр\ \text{BC.}\ \]
\[2)\ \angle ABD = \frac{1}{2} \cup AB = \angle ACB.\]
\[3)\ \mathrm{\Delta}BAC - прямоугольный,\ \]
\[так\ как\ \angle\text{CAB\ }опирается\ \]
\[на\ диаметр:\]
\[\angle A = 90{^\circ};\]
\[4)\ \mathrm{\Delta}\text{ADB\ }и\ \mathrm{\Delta}BAC -\]
\[прямоугольные;\ \ \]
\[\mathrm{\Delta}ADB\sim\mathrm{\Delta}BAC\ (по\ двум\ углам):\]
\[\angle ABD = \angle BCA.\ \]
\[Отсюда:\]
\[\frac{\text{AD}}{\text{AB}} = \frac{\text{AB}}{\text{BC}}\]
\[\frac{AB^{2}}{\text{AD}} = BC = 2r.\]
\[5)\ A\ лежит\ на\ диаметре \Longrightarrow\]
\[\Longrightarrow AD = AB = 2r:\]
\[\frac{AB^{2}}{\text{AD}} = 2r.\]
\[6)\ \frac{AB^{2}}{\text{AD}} = 2r \Longrightarrow \ постоянно\ \]
\[равно\ диаметру.\]
\[Что\ и\ требовалось\ доказать.\]
