Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 879
Задание 879
\[\boxed{\mathbf{879.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[Окружность\ (O;R);\]
\[\cup AB_{1} = \cup B_{1}B = \frac{1}{2} \cup AB;\]
\[\cup AC_{1} = \cup C_{1}C = \frac{1}{2} \cup AC;\]
\[AB \cap B_{1}C_{1} = M;\]
\[AC \cap B_{1}C_{1} = N.\]
\[\mathbf{Доказать:}\]
\[AM = AN.\]
\[\mathbf{Доказательство.}\]
\[1)\ \cup AB_{1} = \cup B_{1}B = \frac{1}{2} \cup AB:\]
\[\angle B_{1}AB = \angle B_{1}BA = \angle B_{1}C_{1}\text{A.}\]
\[2)\ \cup AC_{1} = \cup C_{1}C = \frac{1}{2} \cup AC:\]
\[\angle C_{1}AC = \angle C_{1}CA = \angle C_{1}B_{1}\text{A.}\]
\[3)\ \angle AB_{1}M = \angle C_{1}\text{AN\ }и\ \]
\[\angle B_{1}AM = \angle AC_{1}N:\]
\[\angle AMB_{1} = \angle ANC_{1}.\]
\[4)\ \angle AMN = 180{^\circ} - AMB_{1}\ и\ \]
\[\angle ANM = 180{^\circ} - ANC_{1}:\]
\[\angle AMN = \angle ANM;\]
\[\mathrm{\Delta}AMN - равнобедренный \Longrightarrow\]
\[\Longrightarrow AM = AN.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{879.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AA_{1},\ BB_{1},\ CC_{1} - медианы;\]
\[\mathrm{\Delta}EFG;\]
\[GE = AA_{1};\]
\[GF = BB_{1} = FE = CC_{1}.\]
\[\mathbf{Доказать:}\]
\[\frac{S_{\text{EFG}}}{S_{\text{ABC}}} = \frac{3}{4}.\]
\[\mathbf{Доказательство.}\]
\[1)\ Для\ построения\ проведем\ \]
\[AD \parallel BB_{1}\ и\ \text{BD} \parallel АС.\ \]
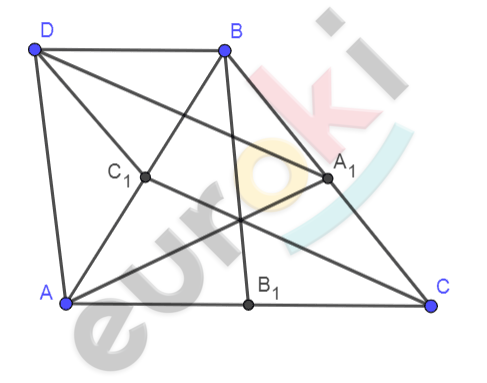\(По\ построению\ \)
\[четырехугольник\ \text{ADB}B_{1}\ - \ \]
\[параллелограмм:\ \]
\[\ \text{AD}\ = \ BB_{1},\]
\[\text{BD}\ = \ AB_{1} = \frac{1}{2}\ AC = \ A_{1}C_{1}.\ \]
\[Точка\ C_{1}\ делит\ диагональ\ \]
\[\text{AB\ }пополам.\ \]
\[Значит,\ она\ делит\ и\ вторую\ \]
\[диагональ\ B_{1}\text{D\ }пополам:\]
\[C_{1}D = \frac{1}{2}B_{1}D = \frac{1}{2}\text{BC.}\]
\[Четырехугольник\ \text{BD}B_{1}C - \ \]
\[параллелограмм:\]
\[\text{BD} \parallel AC\ и\ \text{BD}\ = \ B_{1}C\ = \frac{1}{2}\text{AC.}\]
\[Четырехугольник\ DC_{1}CA_{1} - \ \]
\[параллелограмм:\]
\[\ DC_{1} \parallel A_{1}C,DC_{1}\ = \ A_{1}C \Longrightarrow\]
\[\Longrightarrow DA_{1} = \ CC_{1}.\]
\[\mathrm{\Delta}ADA_{1} - искомый,\]
\[построенный\ на\ медианах\ \]
\[треугольника\ \text{ABC}:\]
\[\text{AD}\ = \ BB_{1};\]
\[DA_{1} = CC_{1},\ \]
\[2)\ Площадь\ \mathrm{\Delta}ADA_{1}:\]
\[S = S_{AC_{1}D} + S_{AC_{1}A_{1}} + S_{A_{1}C_{1}D} =\]
\[= \frac{1}{2}S_{\text{ABD}} + \frac{1}{2}S_{\text{AB}A_{1}} + S_{A_{1}C_{1}B},\]
\[\mathrm{\Delta}ABD = \mathrm{\Delta}AAB_{1},\ в\ котором\ \]
\[основание\ в\ два\ раза\ меньше\ \]
\[основания\ \mathrm{\Delta}\text{ABC},\ а\ высота\ \]
\[та\ же.\ \]
\[\mathrm{\Delta}ABA_{1}\ также\ имеет\ основание\]
\[\ в\ два\ раза\ меньше,\ чем\ \mathrm{\Delta}ABC,\]
\[\ и\ ту\ же\ высоту.\]
\[У\ \mathrm{\Delta}A_{1}C_{1}B\ в\ два\ раза\ меньше\ \]
\[как\ основание,\ так\ и\ высота.\]
\[3)\ Получаем:\]
\[S =\]
\[= \frac{1}{2}S_{\text{AB}B_{1}} + \frac{1}{2} \bullet \frac{1}{2}S_{\text{ABC}} + \frac{1}{4}S_{\text{ABC}} =\]
\[= \frac{1}{4}S_{\text{ABC}} + \frac{1}{4}S_{\text{ABC}} + \frac{1}{4}S_{\text{ABC}} =\]
\[= \frac{3}{4}S_{\text{ABC}}.\]
\[4)\ По\ построению\ \mathrm{\Delta}ADA_{1} =\]
\[= \mathrm{\Delta}EFG - их\ площади\ равны:\ \]
\[\frac{S_{\text{EFG}}}{S_{\text{ABC}}} = \frac{S}{S_{\text{ABC}}} = \frac{3}{4}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
