Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 855
Задание 855
\[\boxed{\mathbf{855.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\ \]
\[\angle C = 90{^\circ};\]
\[CD\bot AB;\]
\[DE\bot AC;\]
\[DF\bot BC.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ CD^{3} = AB \cdot AE \cdot BF\]
\[\textbf{б)}AE^{2} + BF^{2} + 3CD^{2} = AB^{2}\]
\[\textbf{в)}\ \sqrt[3]{AE^{2}} + \sqrt[3]{BF^{2}} = \sqrt[3]{AB^{2}}\]
\[\mathbf{Доказательство.}\]
\[Подобные\ треугольники,\ \]
\[полученные\ в\ результате\ \]
\[построения:\ \]
\[\mathrm{\Delta}ABC\sim\mathrm{\Delta}ADE\sim\mathrm{\Delta}ACD\sim\mathrm{\Delta}DCB\sim\mathrm{\Delta}DBF.\]
\[\textbf{а)}\ \frac{\text{AD}}{\text{CD}} = \frac{\text{CD}}{\text{BD}} \Longrightarrow CD^{2} = AD \cdot BD;\]
\[\frac{\text{AB}}{\text{BC}} = \frac{\text{AC}}{\text{CD}} \Longrightarrow CD = \frac{AC \cdot BC}{\text{AB}};\]
\[\frac{\text{AD}}{\text{AC}} = \frac{\text{DE}}{\text{CD}} \Longrightarrow CD = \frac{AC \cdot DE}{\text{AD}};\]
\[CD =\]
\[= AD \cdot BD \cdot \frac{AC \cdot BC}{\text{AB}} \cdot \frac{AC \cdot DE}{\text{AD}} =\]
\[= AC^{2} \cdot BD \cdot BC \cdot \frac{\text{DE}}{\text{AB}}.\]
\[\frac{\text{AC}}{\text{AD}} = \frac{\text{AB}}{\text{AC}} \Longrightarrow AC^{2} = AB \cdot AD;\]
\[CD^{4} = AD \cdot BD \cdot DC \cdot DE.\]
\[\frac{\text{AD}}{\text{AB}} = \frac{\text{DE}}{\text{BC}} \Longrightarrow AD \cdot BC = AB \cdot DE;\]
\[\frac{\text{DE}}{\text{BF}} = \frac{\text{AE}}{\text{DF}} \Longrightarrow DE = \frac{AE \cdot BF}{\text{DF}};\]
\[CD^{4} = AB \cdot BD \cdot DE^{2} =\]
\[= AB \cdot BD \cdot DE \cdot \frac{AE \cdot BF}{\text{DF}} =\]
\[= AB \cdot AE \cdot BF \cdot \frac{BD \cdot DE}{\text{DF}} =\]
\[= AB \cdot AE \cdot BF \cdot \frac{AC \cdot DE}{\text{AD}} =\]
\[= AB \cdot AE \cdot BF \cdot CD.\]
\[CD^{3} = AB \cdot AE \cdot BF.\]
\[\textbf{б)}\ CD^{2} = AD \cdot BD + теорема\ \]
\[Пифагора:\ \]
\[AB^{2} = (AD + BD)^{2} =\]
\[= AD^{2} + BD^{2} + 2AD \cdot BD =\]
\[= AD^{2} + BD^{2} + 2CD^{2} =\]
\[= AE^{2} + BF^{2} + 3CD^{2}.\]
\[\textbf{в)}\ \frac{\text{AD}}{\text{AE}} = \frac{\text{AB}}{\text{AC}} \Longrightarrow AD = \frac{AB \cdot AE}{\text{AC}}.\]
\[\frac{\text{AC}}{\text{AD}} = \frac{\text{AD}}{\text{AE}} \Longrightarrow AD^{2} = AC \cdot AE.\]
\[AD^{3} = \frac{AB \cdot AE}{\text{AC}} \cdot AC \cdot AE =\]
\[= AB \cdot AE^{2}.\]
\[\frac{\text{AB}}{\text{BD}} = \frac{\text{BC}}{\text{BF}} \Longrightarrow \ BD = \frac{AB \cdot BF}{\text{BC}}.\]
\[\frac{\text{BC}}{\text{BD}} = \frac{\text{BD}}{\text{BF}} \Longrightarrow BD^{2} = BC \cdot BF.\]
\[BD^{3} = \frac{AB \cdot BF}{\text{BC}} \cdot BC \cdot BF =\]
\[= AB \cdot BF^{2}.\]
\[AB = AD + BD =\]
\[= \sqrt[3]{AB \cdot AE^{2}} + \sqrt[3]{AB \cdot BF^{2}}\ \ \ |\ :\sqrt[3]{\text{AB}}\]
\[\sqrt[3]{AB^{2}} = \sqrt[3]{AE^{2}} + \sqrt[3]{BF^{2}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{855.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
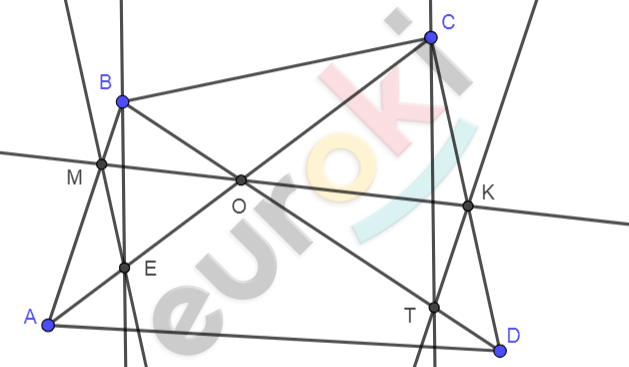
\[ABCD - четырехугольник;\]
\[O = AC \cap BD;\]
\[O \in MK;M \in AB;\]
\[K \in CD;KT \parallel AB;\]
\[T = KT \cap BD;\]
\[ME \parallel CD;\ \]
\[E = ME \cap AC.\]
\[\mathbf{Доказать:}\]
\[BE \parallel CT.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}KTO\sim\mathrm{\Delta}MBO -\]
\[по\ двум\ углам:\]
\[KTO\ и\ MBO:\]
\[KT \parallel AB;\ \ M \in AB;\]
\[BD - секущая \Longrightarrow\]
\[\Longrightarrow \angle KTO = \angle MBO -\]
\[как\ накрест\ лежащие;\]
\[Следовательно:\ \ k = \frac{\text{KO}}{\text{OM}}.\]
\[2)\ \mathrm{\Delta}KCO\sim\mathrm{\Delta}MEO -\]
\[по\ двум\ углам:\]
\[\angle KOC =\]
\[= \angle MOE\ (как\ вертикальные);\]
\[ME \parallel CD;\ \ K \in CD;\ \ \]
\[AC - секущая \Longrightarrow\]
\[\Longrightarrow \angle KCO =\]
\[= \angle MEO\ (как\ накрест\ лежащие).\]
\[Отсюда:\ \ \ k = \frac{\text{KO}}{\text{OM}}\text{.\ }\]
\[Вывод:две\ пары\ \]
\[треугольников\ подобны,\]
\[\ имеют\ один\ и\ тот\ же\ \]
\[коэффициент.\]
\[3)\ \mathrm{\Delta}COT\sim\mathrm{\Delta}EOB - по\ третьему\ \]
\[признаку\ подобия\ \]
\[треугольников:\]
\[\mathrm{\Delta}KTO\sim\mathrm{\Delta}MBO \Longrightarrow\]
\[\Longrightarrow \ k = \frac{\text{KO}}{\text{OM}};\ \ \frac{\text{NO}}{\text{BO}} = k;\]
\[\mathrm{\Delta}KCO\sim\mathrm{\Delta}MEO \Longrightarrow\]
\[\Longrightarrow k = \frac{\text{KO}}{\text{OM}};\ \frac{\text{CO}}{\text{EO}} = k;\]
\[\angle COT =\]
\[= \angle EOB\ (как\ вертикальные).\]
\[Следовательно:\ \ \]
\[\angle CTO = \angle EBO;\ \ так\ как\ \]
\[\text{BD} - секущая\ \ при\ \ \text{BE} \parallel \text{CT.}\ \]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
