Решебник по геометрии 8 класс Атанасян ФГОС Задание 799

 

\[\boxed{\mathbf{799.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

\[\mathbf{Дано:}\]

\[ABCD - равнобедренная\ \]

\[трапеция;\]

\[BH - перпендикуляр\ к\ AD;\ \]

\[AB = CD;\]

\[HD = 7\ см.\]

\[\mathbf{Найти:}\]

\[MN - ?\]

\[\mathbf{Решение.}\]

\[1)\ По\ определению\ средней\ \]

\[линии\ трапеции:\]

\[MN = \frac{1}{2} \bullet (AD + BC).\]

\[2)\ MN - средняя\ линия\ \]

\[трапеции:\]

\[MS - средняя\ линия\ \]

\[треугольника\ \text{ABH.}\]

\[Откуда:\]

\[MS = \frac{1}{2}\text{AH.}\]

\[3)\ PN - средняя\ линия\ \]

\[треугольника\ CFD:\]

\[PN = \frac{1}{2}\text{FD.}\]

\[4)\ \mathrm{\Delta}ABH = \mathrm{\Delta}CFD\ по\ \]

\[гипотенузе\ и\ катету;\]

\[по\ свойству\ равных\ \]

\[треугольников:\]

\[AH = FD.\]

\[5)\ Из\ пункта\ 2\ \ получаем:\]

\[2MS = AH.\]

\[Из\ пункта\ 3:\ \ 2PN = FD.\]

\[Из\ пункта\ 4:\ \ AH = FD.\]

\[Получаем:\ \ \]

\[M = PN;\ \ \]

\[FD = 5M + PN.\]

\[6)\ По\ определению\ \]

\[прямоугольника:\]

\[SP = HF.\]

\[7)\ Теперь\ находим\ среднюю\ \]

\[линию\ трапеции:\ \]

\[MN = MS + SP + PN =\]

\[= FD + HF = HD = 7\ см.\]

\[Ответ:MN = 7\ см.\]

\[\boxed{\mathbf{799.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

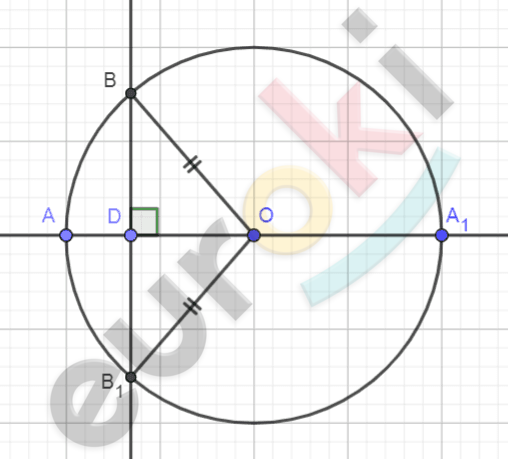
\[\mathbf{Дано:}\]

\[окружность\ (O;r);\]

\[AA_{1} - диаметр;\]

\[BB_{1} - хорда;\]

\[AA_{1}\bot BB_{1}.\]

\[\mathbf{Доказать:}\]

\[\cup AB = \cup AB_{1}.\]

\[\mathbf{Доказательство.}\]

\[1)\ BO = OB_{1} = r:\ \]

\[\mathrm{\Delta}BOB_{1} - равнобедренный.\]

\[2)\ AA_{1}\bot BB_{1} \Longrightarrow \angle BDO =\]

\[= \angle ODB_{1} = 90{^\circ}.\]

\[BO = OB_{1};\ \]

\[DO - общий\ катет.\]

\[Отсюда:\]

\[\angle BOD = \angle DOB_{1}.\]

\[4)\ \angle BOD = \cup AB\ и\ \angle DOB_{1} =\]

\[= \cup AB_{1}\ (как\ центральные\ углы);\]

\[\angle BOD = \angle DOB_{1}.\]

\[Значит:\ \]

\[\cup AB = \cup AB_{1}.\]

\[Что\ и\ требовалось\ доказать.\]