Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 611
Задание 611
\[\boxed{\mathbf{611.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AM - медиана;\]
\[ED \cap AM = O;\]
\[ED \parallel BC;\]
\[E \in AB;\]
\[D \in AC.\]
\[\mathbf{Доказать:}\]
\[EO = OD.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}AEO\sim\mathrm{\Delta}BAM\ \]
\[(по\ двум\ углам),:\]
\[\angle BAM - общий;\]
\[\angle AEO = \angle ABM\ \]
\[(как\ соответственные).\]
\[Отсюда:\]
\[\frac{\text{EO}}{\text{BM}} = \frac{\text{AO}}{\text{AM}}\]
\[EO = \frac{AO \bullet BM}{\text{AM}}.\]
\[2)\ \mathrm{\Delta}AOD\sim\mathrm{\Delta}AMC\ \]
\[(по\ двум\ углам):\]
\[\angle MAC - общий;\ \]
\[\angle ADO = \angle ACM\ \]
\[(как\ соответственные).\]
\[Отсюда:\]
\[\frac{\text{OD}}{\text{MC}} = \frac{\text{AO}}{\text{AM}}\]
\[OD = \frac{AO \bullet MC}{\text{AM}}.\]
\[3)\ OD = \frac{AO \bullet MC}{\text{AM}};\]
\[EO = \frac{AO \bullet BM}{\text{AM}};\]
\[BM = MC.\]
\[Следовательно:\ \]
\[OD = EO.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{611}\mathbf{.}\mathbf{еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
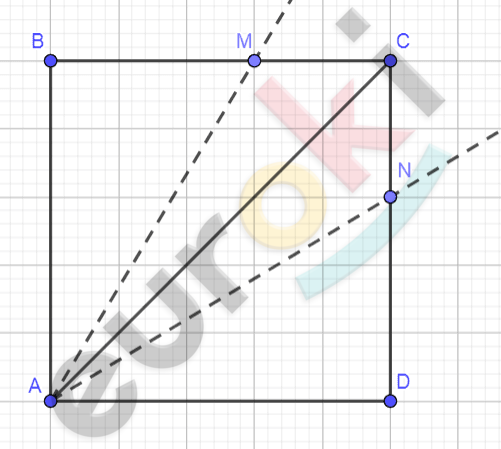
\[Дано:\]
\[ABCD - квадрат.\]
\[Как\ провести\ через\ точку\ \text{A\ }\]
\[две\ прямые\ так,\ чтобы:\]
\[S_{\text{ABM}} = S_{\text{AND}} = S_{\text{AMCN}}.\]
\[Решение.\]
\[1)\ Если\ AB = a:\ \]
\[S_{\text{ABM}} = \frac{1}{2}AB \bullet BM = \frac{1}{2}a \bullet BM;\]
\[S_{\text{ADN}} = \frac{1}{2}AD \bullet DN = \frac{1}{2}a \bullet DN;\]
\[S_{\text{AMCN}} = S_{\text{ABCD}} - S_{\text{ABM}} - S_{\text{ADN}}.\]
\[2)\ Если\ M \in BC \Longrightarrow MB = \frac{2}{3}\text{BC.}\]
\[Если\ N \in CD \Longrightarrow \ DN = \frac{2}{3}\text{CD.}\]
\[\text{AM\ }и\ AN - искомые\ прямые.\]
\[3)\ S_{\text{ABM}} = \frac{1}{2}a \bullet BM;\ \]
\[S_{\text{ADN}} = \frac{1}{2}a \bullet DN;\]
\[S_{\text{AMC}} = \frac{1}{2}a \bullet MC;\]
\[S_{\text{ACN}} = \frac{1}{2}a \bullet CN;\]
\[BM = DN = MC + CN\]
\[BC + CD - необходимо\ \]
\[разделить\ на\ шесть\ равных\ \]
\[частей \Longrightarrow BC\ на\ 3\ равные\ \]
\[части\ и\ \text{DC\ }на\ 3\ равные\ части.\]
\[BM = \frac{2}{3}\text{BC\ }и\ DN = \frac{2}{3}\text{CD.}\]
