Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 574
Задание 574
\[\boxed{\mathbf{574.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ h = \frac{\text{ab}}{c};\]
\[\textbf{б)}\frac{a^{2}}{a_{c}} = \frac{b^{2}}{b_{c}}.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\ S_{\text{ABC}} = \frac{1}{2}\text{ab\ }и\ S_{\text{ABC}} = \frac{1}{2}ch:\]
\[ab = ch\]
\[\ h = \frac{\text{ab}}{c}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ a = \sqrt{a_{c} \bullet c}\]
\[a^{2} = a_{c} \bullet c\]
\[\ c = \frac{a^{2}}{a_{c}}.\]
\[b = \sqrt{b_{c} \bullet c}\]
\[b^{2} = b_{c} \bullet c\]
\[\ c = \frac{b^{2}}{\text{bc}}.\]
\[Получаем:\ \]
\[\frac{a^{2}}{a_{c}} = \frac{b^{2}}{b_{c}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{574.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
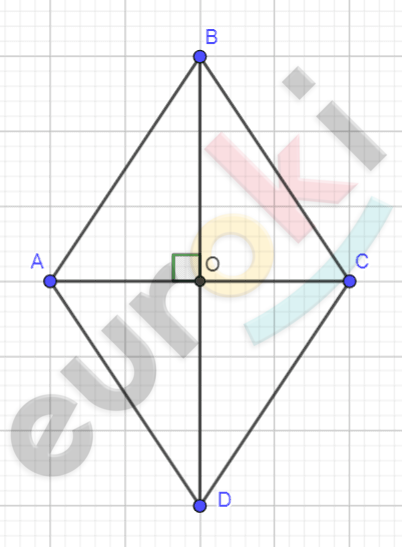
\[\mathbf{Дано:}\]
\[ABCD - ромб;\]
\[\textbf{а)}\ AC = 14\ см;\]
\[BD = 3,2\ дм;\]
\[\textbf{б)}\ AC = 2\ дм;\]
\[BD = 4,6\ дм.\]
\[\mathbf{Доказать:}\]
\[S_{\text{ABCD}} = \frac{BD \bullet AC}{2}.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABCD}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ По\ свойству\ диагоналей\ \]
\[ромба:\]
\[AO = OC;\]
\[BO = OD;\]
\[BD\bot AC.\]
\[Треугольники\ AOD,DOC,AOB,\]
\[BOC - прямоугольные.\]
\[2)\ ⊿AOD = ⊿DOC = ⊿AOB =\]
\[= ⊿BOC\ (по\ двум\ катетам).\]
\[3)\ S_{\text{AOD}} = \frac{1}{2} \bullet \frac{\text{BD}}{2} \bullet \frac{\text{AC}}{2} = \frac{BD \bullet AC}{8}.\]
\[4)\ S_{\text{ABCD}} =\]
\[= S_{\text{AOD}} + S_{\text{DOC}} + S_{\text{AOB}} + S_{\text{BOC}} =\]
\[= 4 \bullet S_{\text{AOD}} = 4 \bullet \frac{BD \bullet AC}{8} =\]
\[= \frac{BD \bullet AC}{2}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{а)}\ S_{\text{ABCD}} = \frac{14 \bullet 32}{2} = 224\ см^{2}.\]
\[\textbf{б)}\ S_{\text{ABCD}} = \frac{2 \bullet 4,6}{2} = 4,6\ дм^{2}.\]
