Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 427
Задание 427
\[\boxed{\mathbf{427}\mathbf{.}\mathbf{ОК}\mathbf{\ }\mathbf{ГДЗ}\mathbf{-}\mathbf{домашка}\mathbf{\ }\mathbf{на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC} - равнобедренный;\]
\[D \in \text{AC};\]
\[\text{ED} \parallel \text{BC}\ и\ \text{DF} \parallel \text{AB}.\]
\[\mathbf{Доказать:}\]
\[P_{\text{BFDE}} = \text{AB} + \text{BC}.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}\text{ABC} - равнобедренный:\]
\[\text{AB} = \text{BC};\ \]
\[\angle A = \angle C.\]
\[2)\ \text{DF} \parallel \text{AB}\ и\ \text{AC} - секущая:\]
\[\angle A =\]
\[= \angle\text{FDC}\ (как\ соответственные);\]
\[\mathrm{\Delta}\text{DFC} - равнобедренный;\]
\[\text{FC} = \text{FD}.\]
\[3)\ \text{FD} \parallel \text{EB}\ и\ \text{BF} \parallel \text{ED}:\]
\[\text{BFDE} - параллелограмм\ \]
\[(по\ определению);\]
\[4)\ \text{BC} \parallel \text{ED}\ и\ \text{AC} - секущая:\]
\[\angle C =\]
\[= \angle\text{EDA}\ (как\ соответственные);\]
\[\mathrm{\Delta}\text{AED} - равнобедренный;\]
\[\text{AE} = \text{ED}.\]
\[5)\ P_{\text{BFDE}} =\]
\[= \text{ED} + \text{BF} + \text{EB} + \text{DF} =\]
\[= 2\text{DF} + 2\text{BF}.\]
\[6)\ \text{AB} = \text{AE} + \text{EB};\]
\[\text{BC} = \text{BF} + \text{FC}:\]
\[P_{\text{BFDE}} = \text{ED} + \text{EB} + \text{BF} + \text{FD} =\]
\[= \text{AE} + \text{EB} + \text{BF} + \text{FC}\]
\[P_{\text{BEFD}} = \text{AB} + \text{BC}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{427.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
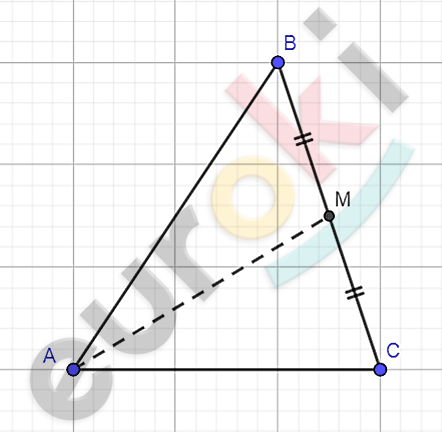
\[AM - медиана;\]
\[AM > \frac{1}{2}\text{BC.}\]
\[\mathbf{Доказать:}\]
\[\angle A < 90{^\circ}.\]
\[\mathbf{Доказательство.}\]
\[3)\ \angle C + \angle B > \angle MAC + \angle MAB \Longrightarrow\]
\[\Longrightarrow \angle C + \angle B > \angle A.\]
\[4)\ Следовательно:\ \]
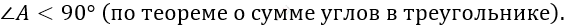
\[Что\ и\ требовалось\ доказать.\]
\[\mathbf{б)\ Дано:}\]
\[\mathrm{\Delta}ABC;\]
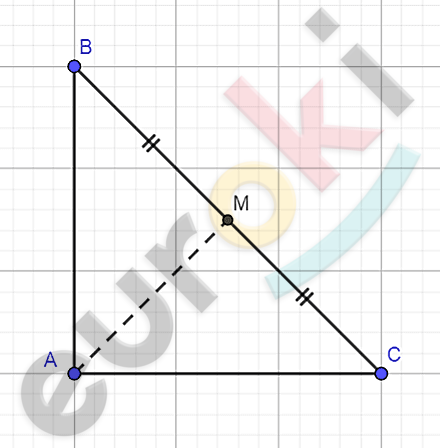
\[AM - медиана;\]
\[AM = \frac{1}{2}\text{BC.}\]
\[\mathbf{Доказать:}\]
\[\angle A = 90{^\circ}.\]
\[\mathbf{Доказательство.}\]
\[1)\ BM = MC = AM:\ \]
\[\mathrm{\Delta}ABM\ и\ \mathrm{\Delta}AMC -\]
\[равнобедренные;\]
\[\angle C = \angle MAC\ и\ \angle B = \angle BAM.\]
\[3)\ \angle C + \angle B = \angle MAC + \angle BAM:\]
\[\angle C + \angle B = \angle A.\]
\[4)\ \angle A + \angle B + \angle C = 180{^\circ}:\]
\[\angle A + \angle A = 180{^\circ}\]
\[2\angle A = 180{^\circ}\]
\[\angle A = 90{^\circ}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\mathbf{в)\ Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AM - медиана;\]
\[AM < \frac{1}{2}\text{BC.}\]
\[\mathbf{Доказать:}\]
\[\angle A > 90{^\circ}.\]
\[\mathbf{Доказательство.}\]
\[3)\ \angle C + \angle B < \angle MAC + \angle MAB:\ \]
\[\angle C + \angle B < \angle A.\]
\[4)\ 180{^\circ} - \angle A < \angle A:\ \]
\[Что\ и\ требовалось\ доказать.\]
