Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 216
Задание 216
\[\boxed{\mathbf{216}\mathbf{.}\mathbf{ОК}\mathbf{\ }\mathbf{ГДЗ}\mathbf{-}\mathbf{домашка}\mathbf{\ }\mathbf{на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[Дано:\ \]
\[DE - биссекстриса\ \angle\text{ADF}.\]
\[Найти:\]
\[\angle DAE - ?\]
\[\ \angle AED - ?\]
\[\angle ADE - ?\]
\[Решение.\]
\[1)\ Рассмотрим\ ME\ и\ NF,\ \]
\[AC - секущая:\]
\[\angle MAC + \angle NCA = 78{^\circ} + 102{^\circ} =\]
\[= 180{^\circ}\ (как\ односторонние).\ \]
\[Значит:\ \]
\[2)\ \angle ADE + \angle EDF + \angle ADC =\]
\[= 180{^\circ}\ (как\ смежные);\]
\[\angle ADF = 180{^\circ} - 48{^\circ} = 132{^\circ};\]
\[\angle ADE = \angle EDF = \frac{\angle ADF}{2} =\]
\[= \frac{132{^\circ}}{2} = 66{^\circ}\ \]
\[\left( так\ как\ \text{DE} - биссектриса \right)\text{.\ }\]
\[3)\ \angle EAD = \angle ADC =\]
\[= 48{^\circ}\ (как\ накрестлежащие).\]
\[4)\ \angle AED = 180{^\circ} - 48{^\circ} - 66{^\circ} =\]
\[= 66{^\circ}\ (по\ теореме\ о\ сумме\ углов).\]
\[Ответ:\ \angle DAE = 48{^\circ};\ \ \]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \angle AED = \angle ADE = 66{^\circ}.\]
\[\boxed{\mathbf{216.еуроки - ответы\ на\ пятёрку}}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[a \parallel b;\]
\[c - секущая;\]
\[AA_{1} - биссектриса\ \angle A;\]
\[BB_{1} - биссектриса\ \angle B.\]
\[\mathbf{Доказать:}\]
\[A_{1} \parallel BB_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ a \parallel b:\]
\[2)\ AA_{1}\ и\ BB_{1} - бисектриссы:\]
\[\angle 1 = \angle 2 = \angle 3 = \angle 4.\]
\[3)\ \angle 2\ и\ \angle 3 - накрестлежащие\ \]
\[(AA_{1}\ и\ BB_{1}\ и\ c - секущая);\]
\[\angle 2 = \angle 3:\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\textbf{б)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[a \parallel b;\]
\[c - секущая;\]
\[AA_{1} - биссектриса\ \angle A;\]
\[BB_{1} - биссектриса\ \angle B.\]
\[Доказать:\]
\[AA_{1}\bot BB_{1}.\]
\[Доказательство.\]
\[1)\ a \parallel b:\ \]
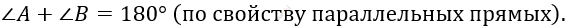
\[2)\ AA_{1}\ и\ BB_{1} - бисектриссы,\ \]
\[следовательно:\]
\[\angle 1 = \angle 2;\ \angle 3 = \angle 4.\]
\[3)\ Рассмотрим\ \mathrm{\Delta}AB_{1}B:\]
\[\angle 1 + \angle 3 + \angle B_{1} = 180{^\circ}\ \]
\[(по\ теореме\ у\ сумме\ углов);\]
\[\frac{1}{2}(\angle A + \angle B) + \angle B_{1} = 180{^\circ};\]
\[\frac{1}{2} \bullet 180{^\circ} + \angle B_{1} = 180{^\circ};\]
\[90{^\circ} + \angle B_{1} = 180{^\circ};\]
\[\angle B_{1} = 90{^\circ}.\]
\[Следовательно:\ \]
\[AA_{1}\bot BB_{1}.\]
\[Что\ и\ требовалось\ доказать.\]
