Решебник по геометрии 8 класс Атанасян ФГОС Задание 1430

\[\boxed{\mathbf{1430.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[BD - биссекриса.\]

\[\mathbf{Доказать:}\]

\[BD^{2} = AB \bullet BC - AD \bullet DC.\]

\[\mathbf{Доказательство.}\]

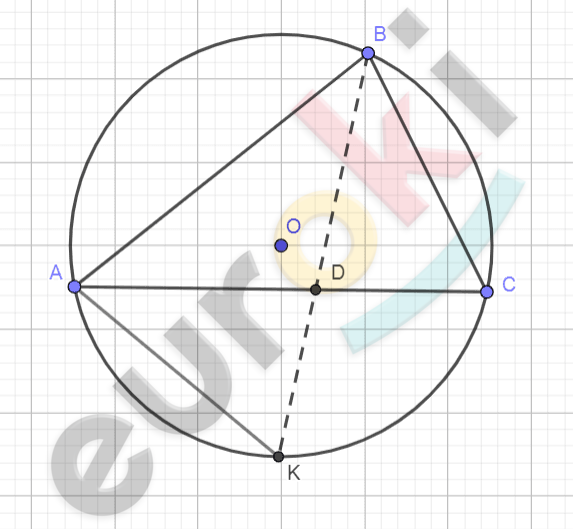
\[1)\ Построим\ описанную\ \]

\[вокруг\ \mathrm{\Delta}ABC\ окружность\ \]

\[(O;R).\]

\[2)\ Продолжим\ луч\ \text{BD\ }\]

\[и\ найдем\ точку\ пересечения\ \]

\[K = (O;R) \cap BD.\]

\[3)\ \mathrm{\Delta}ABK\sim\mathrm{\Delta}BDC -\]

\[по\ двум\ углам:\]

\[\angle ABK =\]

\[= \angle DBC\ (BD - биссектриса);\ \]

\[\angle AKB = \angle ABC = \frac{1}{2} \cup AB.\]

\[Отсюда:\]

\[\frac{\text{AB}}{\text{BD}} = \frac{\text{BK}}{\text{BC}}.\]

\[4)\ BD \bullet BK = AB \bullet BC\]

\[BD \bullet (BD + DK) = AB \bullet BC\]

\[BD^{2} = AB \bullet BC - BD \bullet DK.\]

\[5)\ По\ свойству\]

\[пересекающихся\ хорд:\]

\[BD \bullet DK = AD \bullet DC\]

\[BD^{2} = AB \bullet BC - AD \bullet DC.\ \]

\[Что\ и\ требовалось\ доказать.\]