Решебник по геометрии 8 класс Атанасян ФГОС Задание 1407

\[\boxed{\mathbf{1407.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[ABCD - квадрат;\]

\[\mathrm{\Delta}A_{1}B_{1}C_{1} - правильный.\]

\[\mathbf{Доказать:}\]

\[AB + A_{1}B_{1} \approx \frac{1}{2}C\]

\[с\ точностью\ 0,01R.\]

\[\mathbf{Доказательство.}\]

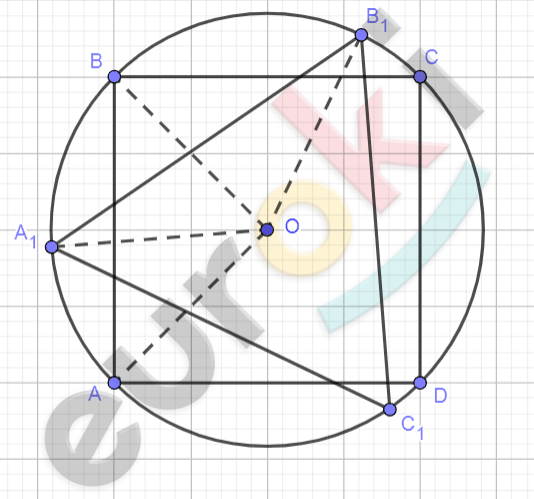
\[1)\ AB = R\sqrt{2} - сторона\ \]

\[квадрата.\]

\[A_{1}B_{1} = R\sqrt{3} - сторона\ \]

\[треугольника.\]

\[AB + A_{1}B_{1} = R\sqrt{2} + R\sqrt{3} =\]

\[= R\left( \sqrt{2} + \sqrt{3} \right)\]

\[\ \frac{1}{2}C = \pi R.\]

\[2)\ Сравним\ \left( \sqrt{2} + \sqrt{3} \right)\ и\ \pi:\]

\[\left( \sqrt{2} + \sqrt{3} \right)^{2} = 2 + 3 + 2\sqrt{6} =\]

\[= 5 + 2\sqrt{6}\ > \pi^{2}\]

\[2\sqrt{6} > \pi^{2} - 5\]

\[4 \cdot 6 > \left( \pi^{2} - 5 \right)^{2}\]

\[24 > 23,71.\]

\[Относительная\ погрешность:\ \]

\[\delta = \frac{24 - 23,71}{24} \approx 1\%.\]

\[Что\ соответствует\ точности\ \]

\[(абсолютной\ погрешности)\ \]

\[\mathrm{\Delta} = 0,001R.\]

\[Что\ и\ требовалось\ доказать.\]