Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 1094
Задание 1094
\(\boxed{\mathbf{1094.ОК\ ГДЗ - домашка\ на}\ 5}\)
\[\textbf{а)}\ n = 4;R = 3\sqrt{2}\ см:\]
\[1)\ a_{4} = 2 \bullet R \bullet \sin\frac{180{^\circ}}{4} =\]
\[= 2 \bullet 3\sqrt{2} \bullet \sin{45{^\circ}} =\]
\[= 2 \bullet 3\sqrt{2} \bullet \frac{\sqrt{2}}{2} = 6\ см;\]
\[2)\ P = 4 \bullet a_{4} = 4 \bullet 6 = 24\ см;\]
\[3)\ r = R \bullet \cos\frac{180{^\circ}}{4} =\]
\[= 3\sqrt{2} \bullet \cos{45{^\circ}} = 3\sqrt{2} \bullet \frac{\sqrt{2}}{2} =\]
\[= 3\ см;\]
\[4)\ S = \frac{1}{2}P \bullet r = \frac{1}{2} \bullet 24 \bullet 3 =\]
\[= 36\ см^{2}.\]
\[\textbf{б)}\ n = 3;P = 24\ см:\]
\[1)\ P = 3 \bullet a_{3} \Longrightarrow a_{3} = \frac{P}{3} = \frac{24}{3} =\]
\[= 8\ см;\]
\[2)\ 8 = 2R \bullet \sin\frac{180{^\circ}}{3}\]
\[8 = 2R \bullet \sin{60{^\circ}}\]
\[8 = 2R \bullet \frac{\sqrt{3}}{2}\ \]
\[8 = R\sqrt{3}\]
\[R = \frac{8}{\sqrt{3}}\ см;\]
\[3)\ r = R \bullet \cos\frac{180{^\circ}}{3} =\]
\[= \frac{8}{\sqrt{3}} \bullet \cos{60{^\circ}} = \frac{8}{\sqrt{3}} \bullet \frac{1}{2} = \frac{4}{\sqrt{3}}\ см;\]
\[4)\ S = \frac{1}{2}P \bullet r = \frac{1}{2} \bullet 24 \bullet \frac{4}{\sqrt{3}} =\]
\[= \frac{48}{\sqrt{3}} = \frac{48\sqrt{3}}{3} = 16\sqrt{3}\ см^{2}.\]
\[\textbf{в)}\ n = 6;r = 9\ см:\]
\[1)\ r = R \bullet \cos\frac{180{^\circ}}{n}\]
\[9 = R \bullet \cos\frac{180{^\circ}}{6}\]
\[9 = R \bullet \cos{30{^\circ}}\]
\[9 = R\frac{\sqrt{3}}{2}\]
\[18 = R\sqrt{3}\]
\[R = \frac{18}{\sqrt{3}}\ см;\]
\[2)\ a_{6} = 2 \bullet \frac{18}{\sqrt{3}} \bullet \sin\frac{180{^\circ}}{6} =\]
\[= 2 \bullet \frac{18}{\sqrt{3}} \bullet \sin{30{^\circ}} = 2 \bullet \frac{18}{\sqrt{3}} \bullet \frac{1}{2} =\]
\[= \frac{18}{\sqrt{3}}\ см;\]
\[3)\ P = 6 \bullet \frac{18}{\sqrt{3}} = 6 \bullet \frac{18}{3} \bullet \sqrt{3} =\]
\[= 36\sqrt{3}\ см;\]
\[4)\ S = \frac{1}{2} \bullet P \bullet r = \frac{1}{2} \bullet 36\sqrt{3} \bullet 9 =\]
\[= 162\sqrt{3}\ см^{2}.\]
\[\textbf{г)}\ n = 8;r = 5\sqrt{3}\ см:\]
\[1)\ r = R \bullet \cos\frac{180{^\circ}}{8}\]
\[5\sqrt{3} = R \bullet \cos{22{^\circ}30^{'}}\]
\[R = \frac{5\sqrt{3}}{\cos{22{^\circ}30^{'}}}\ см;\]
\[2)\ a_{6} =\]
\[= 2 \bullet \frac{5\sqrt{3}}{\cos{22{^\circ}30^{'}}} \bullet \sin{22{^\circ}30^{'}} =\]
\[= 10\sqrt{3} \bullet tg\ 22{^\circ}30'\ см;\]
\[3)\ P = 8 \bullet 10\sqrt{3} \bullet tg\ 22{^\circ}30^{'} =\]
\[= 8 \bullet 10\sqrt{3} \bullet 0,4142 \approx\]
\[\approx 33,136\sqrt{3}\ см;\]
\[4)\ S = \frac{1}{2} \bullet P \bullet r =\]
\[= \frac{1}{2} \bullet 33,136\sqrt{3} \bullet 5\sqrt{3} =\]
\[= 248,52\ см^{2}.\]
\[\boxed{\mathbf{1094.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
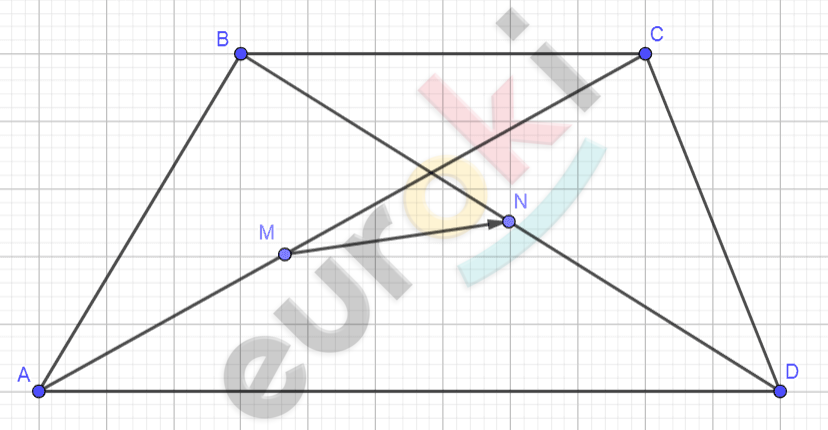
\[\mathbf{Дано:}\]
\[ABCD - трапеция;\]
\[M \in AC;AM = MC;\]
\[N \in BD;BN = ND.\]
\[\mathbf{Доказать:}\]
\[MN = \frac{1}{2}(AD - BC).\]
\[\mathbf{Доказательство.}\]
\[1)\ По\ правилу\ \]
\[многоугольника:\]
\[\overrightarrow{\text{MN}} = \overrightarrow{\text{MA}} + \overrightarrow{\text{AD}} + \overrightarrow{\text{DN}};\]
\[\overrightarrow{\text{MN}} = \overrightarrow{\text{MC}} + \overrightarrow{\text{CB}} + \overrightarrow{\text{BN}}.\]
\[3)\ N\ и\ M - середины\ \text{BD\ }и\ AC:\]
\[\overrightarrow{\text{MA}} + \overrightarrow{\text{MC}} = \overrightarrow{0};\ \ \ \]
\[\overrightarrow{\text{DN}} + \overrightarrow{\text{BN}} = \overrightarrow{0}.\]
\[4)\ 2\overrightarrow{\text{MN}} = \overrightarrow{\text{AD}} + \overrightarrow{\text{CB}}\]
\[2\overrightarrow{\text{MN}} = \overrightarrow{\text{AD}} - \overrightarrow{\text{BC}}\]
\[\overrightarrow{\text{MN}} = \frac{1}{2}\left( \overrightarrow{\text{AD}} - \overrightarrow{\text{BC}} \right).\]
\[5)\ \frac{\overrightarrow{\text{AD}} \uparrow \uparrow \overrightarrow{\text{BC}}}{\overrightarrow{\text{MN}} \uparrow \uparrow \overrightarrow{\text{AD}}}\]
\[\left| \overrightarrow{\text{AD}} - \overrightarrow{\text{BC}} \right| = AD - BC\]
\[MN = \frac{1}{2}(AD - BC).\]
\[Что\ и\ требовалось\ доказать.\]
