Решебник по геометрии 8 класс Атанасян ФГОС Вопросы для повторения к главе I

\[\boxed{Вопросы\ для\ повторения\ к\ глав\mathbf{е\ І.\ }\mathbf{еуроки - ответы\ на\ пятёрку}\mathbf{\ }}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Через\ две\ точки\ на\ плоскости\ }\]

\[\mathbf{можно\ провести\ только\ одну\ }\]

\[\mathbf{прямую.}\]

\[\boxed{\mathbf{2.}}\]

\[\mathbf{Две\ прямые\ могут\ иметь\ одну\ }\]

\[\mathbf{общую\ точку:}\]

\[\mathbf{Или\ не\ иметь\ общих\ точек:}\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Отрезок - это\ часть\ прямой,\ }\]

\[\mathbf{ограниченная\ двумя\ точками.}\]

\[\boxed{\mathbf{4.}}\]

\[\mathbf{Ломаная - геометрическая\ }\]

\[\mathbf{фигура,\ составленная\ из\ }\]

\[\mathbf{отрезков\ так,\ что\ смежные\ }\]

\[\mathbf{отрезки\ не\ лежат\ на\ одной\ }\]

\[\mathbf{прямой.}\]

\[\mathbf{Звенья - отрезки,\ из\ которых\ }\]

\[\mathbf{состоит\ ломаная.}\]

\[\mathbf{Вершины\ ломаной - концы}\]

\[\mathbf{звеньев.}\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Многоугольник - замкнутая\ }\]

\[\mathbf{ломаная,\ несмежные\ звенья\ }\]

\[\mathbf{которой\ не\ имеют\ общих\ }\]

\[\mathbf{точек.}\]

\[\boxed{\mathbf{6.}}\]

\[\mathbf{Луч - это\ часть\ прямой,\ }\]

\[\mathbf{имеющая\ начальную\ точку.}\]

\[\mathbf{Обозначают\ луч\ либо\ одной\ }\]

\[\mathbf{малой\ латинской\ буквой\ }\left( \mathbf{a} \right)\mathbf{,\ }\]

\[\mathbf{либо\ двумя\ большими\ }\]

\[\mathbf{латинскими\ буквами,\ }\]

\[\mathbf{где\ первая\ буква\ обозначает}\]

\[\mathbf{начальную\ точку\ }\left( \mathbf{\text{AB}} \right)\mathbf{.}\]

\[\boxed{\mathbf{7.}}\]

\[\mathbf{Угол - это\ геометрическая\ }\]

\[\mathbf{фигура,\ которая\ состоит\ }\]

\[\mathbf{из\ точки\ и\ двух\ лучей,\ }\]

\[\mathbf{исходящих\ из\ этой\ точки.\ }\]

\[\mathbf{Лучи\ называют\ сторонами\ }\]

\[\mathbf{угла,их\ общее\ начало -}\]

\[\mathbf{вершиной\ угла.}\]

\[\boxed{\mathbf{8.}}\]

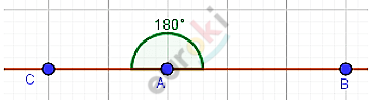
\[\mathbf{Угол\ называют\ развернутым,}\]

\[\mathbf{если\ обе\ его\ стороны\ лежат\ }\]

\[\mathbf{на\ одной\ прямой.}\]

\[\boxed{\mathbf{9.}}\]

\[\mathbf{Две\ геометрические\ фигуры\ }\]

\[\mathbf{называются\ равными,\ если\ }\]

\[\mathbf{их\ можно\ совместить\ }\]

\[\mathbf{наложением.}\]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Чтобы\ сравнить\ два\ отрезка,\ }\]

\[\mathbf{нужно\ наложить\ один\ отрезок\ }\]

\[\mathbf{на\ другой,\ при\ этом\ конец\ }\]

\[\mathbf{одного\ отрезка\ должен\ }\]

\[\mathbf{совпасть\ с\ одним\ из\ концов\ }\]

\[\mathbf{другого.\ }\]

\[\mathbf{Если\ при\ этом\ совпадают\ и\ }\]

\[\mathbf{вторые\ концы,\ то\ такие\ }\]

\[\mathbf{отрезки\ считаются\ равными.\ }\]

\[\mathbf{Если\ вторые\ концы\ }\]

\[\mathbf{не\ совпадают,\ то\ отрезок,}\]

\[\mathbf{который\ составляет\ часть\ }\]

\[\mathbf{другого,\ считается\ меньшим.}\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Середина\ отрезка - это\ точка,\ }\]

\[\mathbf{делящая\ его\ пополам:то\ есть\ }\]

\[\mathbf{на\ два\ равных\ отрезка.}\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Чтобы\ сравнить\ углы,\ можно\ }\]

\[\mathbf{наложить\ их\ друг\ на\ друга\ так,\ }\]

\[\mathbf{чтобы\ их\ вершины\ оказались\ }\]

\[\mathbf{в\ одной\ точке\ и\ одна\ сторона\ }\]

\[\mathbf{первого\ угла\ совпала\ с\ одной\ }\]

\[\mathbf{стороной\ второго\ угла.\ }\]

\[\mathbf{При\ этом\ несовмещённые\ }\]

\[\mathbf{стороны\ должны\ оказаться\ }\]

\[\mathbf{рядом\ друг\ с\ другом\ —\ по\ одну\ }\]

\[\mathbf{сторону\ от\ совмещённых\ }\]

\[\mathbf{сторон.\ }\]

\[\mathbf{Если\ несовмещённые\ стороны\ }\]

\[\mathbf{углов\ совпали,\ то\ углы\ равны.}\]

\[\boxed{\mathbf{13.}}\]

\[\mathbf{Биссектриса - это\ луч,\ }\]

\[\mathbf{исходящий\ из\ вершины\ угла\ и\ }\]

\[\mathbf{делящий\ его\ на\ два\ равных\ }\]

\[\mathbf{угла.}\]

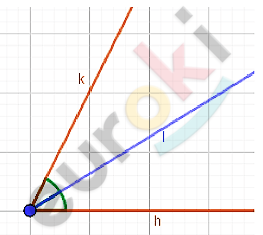
\[l - биссектриса\ \angle(k;h).\]

\[\boxed{\mathbf{14.}}\]

\[Так\ как\ точка\ \text{C\ }принадлежит\ \]

\[отрезку\ \text{AB},\ то\ она\ разбивает\ \]

\[его\ на\ две\ части:отрезки\ \text{AC\ }\]

\[и\ \text{CB.}\]

\[Следовательно,\ длина\ \]

\[отрезка\ AB\ равна\ сумме\ длин\ \]

\[отрезков\ \text{AC\ }и\ CB:\]

\[AB = AC + CB.\]

\[\boxed{\mathbf{15.}}\]

\[\mathbf{Длина\ ломаной - это\ сумма\ }\]

\[\mathbf{длин\ всех\ ее\ звеньев.}\]

\[\boxed{\mathbf{16.}}\]

\[\mathbf{Наименьшее\ число\ сторон\ }\]

\[\mathbf{многоугольника\ равно\ 3.}\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{Периметр\ многоугольника -}\]

\[\mathbf{это\ сумма\ длин\ всех\ его\ }\]

\[\mathbf{сторон.}\]

\[\boxed{\mathbf{18.}}\]

\[\mathbf{Приборы\ для\ измерения\ }\]

\[\mathbf{расстояний:}\]

\[\mathbf{линейка;измерительная\ }\]

\[\mathbf{лентка;рулетка;нивелир;}\]

\[\mathbf{микрометр;штангенциркуль.}\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Градусная\ мера\ угла - это\ }\]

\[\mathbf{положительное\ число,\ которое\ }\]

\[\mathbf{показывает,сколько\ раз\ градус\ }\]

\[\mathbf{и\ его\ части\ укладываются\ }\]

\[\mathbf{в\ данном\ угле.}\]

\[\boxed{\mathbf{20.}}\]

\[Для\ любого\ луча\ OC \in \angle AOB\ \]

\[справедливо\ равенство:\]

\[\angle AOB = \angle AOC + \angle COB.\]

\[\boxed{\mathbf{21.}}\]

\[Острый\ угол - угол,\ градусная\ \]

\[мера\ которого\ больше\ 0{^\circ}\ \]

\[и\ меньше\ 90{^\circ}.\]

\[Прямой\ угол - угол,\ градусная\ \]

\[мера\ которого\ равна\ 90{^\circ}.\]

\[Тупой\ угол - угол,\ градусная\ \]

\[мерка\ которога\ больше\ 90{^\circ}\ \]

\[и\ меньше\ 180{^\circ}.\]

\[\boxed{\mathbf{22.}}\]

\[\mathbf{Смежными\ называют\ углы,\ }\]

\[\mathbf{у\ которых\ одна\ сторона\ общая,\ }\]

\[\mathbf{а\ две\ другие\ дополняют\ друг\ }\]

\[\mathbf{друга\ до\ прямой.\ Смежные\ }\]

\[\mathbf{углы\ составляют}\]

\[\mathbf{развернутый\ угол.}\]

\[\boxed{\mathbf{23.}}\]

\[\mathbf{Вертикальные\ углы\ - \ это\ }\]

\[\mathbf{пары\ углов,\ имеющие\ общую\ }\]

\[\mathbf{вершину\ и\ образованные\ при\ }\]

\[\mathbf{пересечении\ двух\ прямых\ так,\ }\]

\[\mathbf{что\ стороны\ одного\ угла\ }\]

\[\mathbf{являются\ продолжениями\ }\]

\[\mathbf{другого.}\]

\[\mathbf{Вертикальные\ углы\ равны\ }\]

\[\left( \mathbf{свойство} \right)\mathbf{.}\]

\[\boxed{\mathbf{24.}}\]

\[Перпендикулярные\ прямые -\]

\[это\ прямые,\ которые\ \]

\[пересекаются\ друг\ с\ другом\ \]

\[под\ углом\ 90{^\circ}.\]

\[\boxed{\mathbf{25.}}\]

\[\mathbf{Две\ прямые,\ }\]

\[\mathbf{перпендикулярные\ к\ третьей,\ }\]

\[\mathbf{не\ пересекаются\ потому,}\]

\[\mathbf{что\ они\ друг\ другу\ }\]

\[\mathbf{параллельны.}\]

\[\mathbf{Это\ вытекает\ из\ свойства\ }\]

\[\mathbf{параллельных\ прямых.}\]

\[\boxed{\mathbf{26.}}\]

\[\mathbf{Для\ построения\ прямых\ углов\ }\]

\[\mathbf{на\ местности\ используют\ }\]

\[\mathbf{простейший\ прибор - эккер.\ }\]

\[\mathbf{Более\ совершенные -}\]

\[\mathbf{теодолит,\ буссоль.}\]