Решебник по геометрии 8 класс Мерзляк Задание 185

\[Схематический\ рисунок.\]

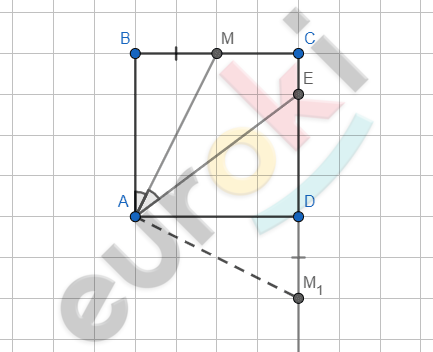
\[Дано:\]

\[ABCD - квадрат;\]

\[\angle BAM = \angle MAE.\]

\[Доказать:\]

\[AE = BM + DE.\]

\[Доказательство.\]

\[1)\ Отметим\ точку\ M_{1}:\]

\[DM_{1} = BM.\]

\[2)\ ABCD - квадрат:\]

\[\angle A = \angle B = \angle D = 90{^\circ};\]

\[AB = AD.\]

\[3)\ \mathrm{\Delta}ABM = \mathrm{\Delta}ADM_{1} - по\ двум\ \]

\[катетам:\]

\[\angle ABM = \angle ADM_{1} = 90{^\circ}.\]

\[Отсюда:\]

\[\angle DAM_{1} = \angle BAM.\]

\[4)\ \mathrm{\Delta}ADM_{1} - прямоугольный:\]

\[\angle DAM_{1} + \angle AM_{1}D = 90{^\circ}\]

\[\angle AM_{1}D = 90{^\circ} - \angle BAM.\]

\[5)\ В\ \mathrm{\Delta}\text{AE}M_{1}:\]

\[\angle EAD = 90{^\circ} - \angle BAM - \angle MAE\]

\[\angle EAD = 90{^\circ} - 2\angle BAM.\]

\[\angle EAM_{1} = \angle EAD + \angle DAM_{1}\]

\[\angle EAM_{1} = 90{^\circ} - \angle BAM\]

\[\angle AM_{1}E = \angle EAM_{1}.\]

\[\mathrm{\Delta}AEM_{1} - равнобедренный:\]

\[EM_{1} = AE.\]

\[6)\ Искомое\ равенство:\]

\[EM_{1} = DE + DM_{1};\]

\[AE = DE + BM.\]

\[Что\ и\ требовалось\ доказать.\]