Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 990
Задание 990
\[\boxed{\mathbf{990.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Дано:\ \]
\[\overrightarrow{a}\left\{ 3;4 \right\};\ \overrightarrow{b}\left\{ 6; - 8 \right\};\ \overrightarrow{c}\left\{ 1;5 \right\};\]
\[\overrightarrow{p} = \overrightarrow{a} + \overrightarrow{b};\ \]
\[\overrightarrow{q} = \overrightarrow{b} + \overrightarrow{c};\ \]
\[\overrightarrow{r} = 2\overrightarrow{a} - \overrightarrow{b} + \overrightarrow{c};\ \]
\[\overrightarrow{s} = \overrightarrow{a} - \overrightarrow{b} - \overrightarrow{c}.\]
\[Найти:\]
\[\textbf{а)}\ координаты\ \overrightarrow{p},\ \overrightarrow{q},\overrightarrow{r}\ и\ \overrightarrow{s};\]
\[\textbf{б)}\ \left| \overrightarrow{a} \right|,\left| \overrightarrow{b} \right|,\left| \overrightarrow{p} \right|\ и\ \left| \overrightarrow{q} \right|.\]
\[Решение.\]
\[\textbf{а)}\ \overrightarrow{p} = \left\{ 3;4 \right\} + \left\{ 6; - 8 \right\} = \left\{ 9; - 4 \right\};\]
\[\overrightarrow{q} = \left\{ 6; - 8 \right\} + \left\{ 1;5 \right\} = \left\{ 7; - 3 \right\};\]
\[\overrightarrow{r} = 2\left\{ 3;4 \right\} - \left\{ 6; - 8 \right\} + \left\{ 1;5 \right\} =\]
\[= \left\{ 6;8 \right\} - \left\{ 6; - 8 \right\} + \left\{ 1;5 \right\} =\]
\[= \left\{ 0;16 \right\} + \left\{ 1;5 \right\} = \left\{ 1;21 \right\}.\]
\[\overrightarrow{s} = \left\{ 3;4 \right\} - \left\{ 6; - 8 \right\} - \left\{ 1;5 \right\} =\]
\[= \left\{ - 3;12 \right\} - \left\{ 1;5 \right\} = \left\{ - 4;7 \right\}.\]
\[\textbf{б)}\ \left| \overrightarrow{a} \right| = \sqrt{9 + 16} = \sqrt{25} = 5;\]
\[\left| \overrightarrow{b} \right| = \sqrt{36 + 64} = \sqrt{100} = 10;\]
\[\left| \overrightarrow{p} \right| = \sqrt{81 + 16} = \sqrt{97};\]
\[\left| \overrightarrow{q} \right| = \sqrt{49 + 9} = \sqrt{58}.\]
\[\boxed{\mathbf{990.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
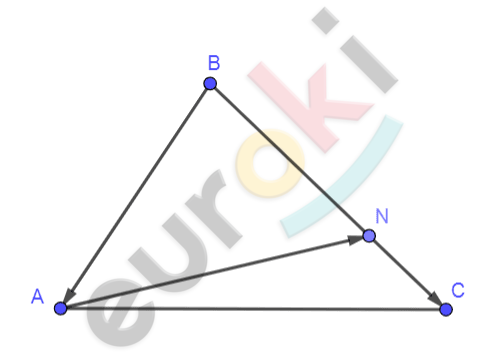
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[BN = 2NC;\]
\[\overrightarrow{a} = \overrightarrow{\text{BA}};\ \]
\[\overrightarrow{b} = \overrightarrow{\text{BC}}.\]
\[\mathbf{Выразить:}\]
\[\overrightarrow{\text{AN}}\ через\ \overrightarrow{a}\ и\ \overrightarrow{b}.\]
\[\mathbf{Решение.}\]
\[1)\ \overrightarrow{\text{BN}} = 2\overrightarrow{\text{NC}}:\]
\[\overrightarrow{\text{BN}} = \frac{2}{3}\overrightarrow{\text{BC}} = \frac{2}{3}\overrightarrow{b}.\]
\[2)\ По\ правилу\ треугольника:\ \ \]
\[\overrightarrow{\text{AN}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BN}} = - \overrightarrow{\text{BA}} + \overrightarrow{\text{BN}} =\]
\[= - \overrightarrow{a} + \frac{2}{3}\overrightarrow{b}.\]
