Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 979
Задание 979
\[\boxed{\mathbf{979.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:}\]
\[A( - 8;6);\]
\[B( - 3; - 1);\]
\[M(5;y);\]
\[M \in AB.\]
\[\mathbf{Найти:}\]
\[\mathbf{Решение.}\]
\[1) - \left\{ \begin{matrix} - 6 - 8k + b \\ - 1 = - 3k + b \\ \end{matrix} \right.\ \Longrightarrow - 5 =\]
\[= - 5k \Longrightarrow k = 1;\]
\[\left\{ \begin{matrix} k = 1 \\ b = 2 \\ \end{matrix} \right.\ .\]
\[2)\ y = x + 2\]
\[y = 5 + 2 = 7\]
\[M(5;7).\]
\[Ответ:\ y = 7.\]
\[\boxed{\mathbf{979}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
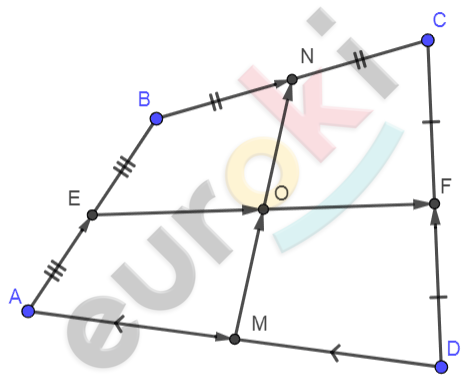
\[\mathbf{Дано:}\]
\[ABCD - четырехугольник;\]
\[BN = NC;CF = FD;\ \]
\[BE = EA;AM = MD;\]
\[EF \cap NM = 0.\]
\[\mathbf{Доказать:}\]
\[NO = OM;\ \ \]
\[EO = OF.\]
\[\mathbf{Доказательство.}\]
\[1) - \overrightarrow{\text{EA}} + \overrightarrow{\text{AM}} + \overrightarrow{\text{MD}} + \overrightarrow{\text{DF}} =\]
\[= \overrightarrow{\text{EO}} + \overrightarrow{\text{OF}}\]
\[- \overrightarrow{\text{EA}} + \overrightarrow{\text{AM}} + \overrightarrow{\text{MO}} = \overrightarrow{\text{EO}}\]
\[- \overrightarrow{\text{EA}} + 2\overrightarrow{\text{AM}} + \overrightarrow{\text{DF}} = \overrightarrow{\text{EO}} + \overrightarrow{\text{OF}}\]
\[- \overrightarrow{\text{EA}} + \overrightarrow{\text{AM}} + \overrightarrow{\text{EO}} = \overrightarrow{\text{EO}}\text{.\ }\]
\[2) - \overrightarrow{\text{MA}} + \overrightarrow{\text{AE}} + \overrightarrow{\text{EB}} + \overrightarrow{\text{BN}} =\]
\[= \overrightarrow{\text{MO}} + \overrightarrow{\text{ON}}\]
\[- \overrightarrow{\text{MA}} + \overrightarrow{\text{AE}} + \overrightarrow{\text{EO}} = \overrightarrow{\text{MO}}\]
\[- \overrightarrow{\text{MA}} + 2\overrightarrow{\text{AE}} + \overrightarrow{\text{BN}} = \overrightarrow{\text{MO}} + \overrightarrow{\text{ON}}\]
\[- \overrightarrow{\text{MA}} + \overrightarrow{\text{AE}} + \overrightarrow{\text{EO}} = \overrightarrow{\text{MO}}.\]
\[3)\ Выразим\ \overrightarrow{\text{EO}}\text{\ \ }и\ \ \ \overrightarrow{\text{MO}};\]
\[подставим:\]
\[- \overrightarrow{\text{EA}} + 2\overrightarrow{\text{AM}} + \overrightarrow{\text{DF}} =\]
\[= - \overrightarrow{\text{EA}} + \overrightarrow{\text{AM}} + \overrightarrow{\text{MO}} + \overrightarrow{\text{OF}}\]
\[- \overrightarrow{\text{MA}} + 2\overrightarrow{\text{AE}} + \overrightarrow{\text{BN}} =\]
\[= - \overrightarrow{\text{MA}} + \overrightarrow{\text{AE}} + \overrightarrow{\text{EO}} + \overrightarrow{\text{ON}}.\]
\[Получим:\]
\[\overrightarrow{\text{AM}} + \overrightarrow{\text{DF}} = \overrightarrow{\text{MO}} + \overrightarrow{\text{OF}}\]
\[\overrightarrow{\text{AE}} + \overrightarrow{\text{BN}} = \overrightarrow{\text{EO}} + \overrightarrow{\text{ON}}.\]
\[4)\ Запишем\ выражения:\]
\[2\overrightarrow{\text{AM}} + 2\overrightarrow{\text{DF}} = \overrightarrow{\text{AC}}\]
\[2\overrightarrow{\text{AE}} + 2\overrightarrow{\text{BN}} = \overrightarrow{\text{AC}}\]
\[Получим\ равенство:\]
\[\overrightarrow{\text{AM}} + \overrightarrow{\text{DF}} = \overrightarrow{\text{AE}} + \overrightarrow{\text{BN}}.\]
\[Следовательно:\]
\[\overrightarrow{\text{MO}} + \overrightarrow{\text{OF}} = \overrightarrow{\text{EO}} + \overrightarrow{\text{ON}}\]
\[\overrightarrow{\text{MO}} - \overrightarrow{\text{ON}} = \overrightarrow{\text{EO}} - \overrightarrow{\text{OF}}.\]
\[5)\ Так\ как\ \ \overrightarrow{\text{MO}} \nearrow \nearrow \overrightarrow{\text{ON}};\ \]
\[\overrightarrow{\text{EO}} \nearrow \nearrow \overrightarrow{\text{OF}};\]
\[\ EO;OF\ \ и\ \ MO;ON;\ \ \ \]
\[то\ не\ \ коллинеарные:\]
\[NO = OM;\ \ EO = OF.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
