Решебник по геометрии 7 класс Атанасян ФГОС Задание 970

 

\[\boxed{\mathbf{970.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[Окружность\ (O;R);\]

\[A(1;3);\ \]

\[A \in (O;R);\]

\[R = 5;\]

\[O \in OX.\]

\[\mathbf{Написать:}\]

\[уравнение\ окружности.\]

\[\mathbf{Решение.}\]

\[1)\ Пусть\ точка\ O\ имеет\ \]

\[координаты\ (x;0):\]

\[R = OA = \ \]

\[= \sqrt{(1 - x)^{2} + (0 - 3)^{2}} =\]

\[= \sqrt{25} = 5\]

\[(1 - x)^{2} + 9 = 5\ \ и\ \ \ \]

\[(1 - x)^{2} = 16;\]

\[x_{1} = - 3\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }x_{2} = 5\]

\[3)\ O_{1}( - 3;0)\ и\ O_{2}(5;0) -\]

\[существуют\ две\ окружности:\]

\[(x - 5)^{2} + y^{2} = 25;\ \]

\[(x + 3)^{2} + y^{2} = 25.\]

\[Ответ:\ (x - 5)^{2} + y^{2} = 25\ и\ \]

\[(x + 3)^{2} + y^{2} = 25.\]

\[\boxed{\mathbf{970.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

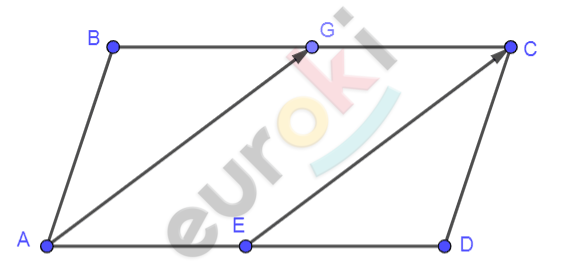
\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[AE = ED;\ \ \]

\[BE = GC.\]

\[\overrightarrow{\text{DC}} = \overrightarrow{a};\ \ \]

\[\overrightarrow{\text{BC}} = \overrightarrow{b}.\]

\[Выразить:\]

\[\overrightarrow{\text{EC}}\ \ \ и\ \ \ \overrightarrow{\text{AG}}.\]

\[\mathbf{Решение.}\]

\[1)\ По\ правилу\ треугольника:\]

\[\overrightarrow{\text{AG}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BG}} = \overrightarrow{\text{DC}} + \overrightarrow{\frac{\text{BC}}{2}} =\]

\[= \overrightarrow{a} + \frac{1}{2}\overrightarrow{b}.\]

\[2)\ По\ правилу\ треугольника:\]

\[\overrightarrow{\text{EC}} = \overrightarrow{\text{ED}} + \overrightarrow{\text{DC}} = \overrightarrow{\frac{\text{AD}}{2}} + \overrightarrow{\text{DC}} =\]

\[= \overrightarrow{\frac{\text{BC}}{2}} + \overrightarrow{\text{DC}} = \frac{1}{2}\overrightarrow{b} + \overrightarrow{a}.\]