Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 961
Задание 961
\[\boxed{\mathbf{961.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дан}о:\]
\[A( - 2;4);B( - 5; - 3);C( - 7; - 2);\]
\[D(1;5);\]
\[(x + 5)^{2} + (y - 1)^{2} = 16 \Longrightarrow\]
\[\Longrightarrow O( - 5;1);\ R = 4.\]
\[1)\ A( - 2;4):\]
\[( - 2 + 5)^{2} + (4 - 1)^{2} \neq 16;\]
\[9 + 9 \neq 16;\]
\[18 \neq 16 \Longrightarrow \ A( - 2;4) - вне\ \]
\[круга.\]
\[2)\ B( - 5; - 3):\]
\[( - 5 + 5)^{2} + ( - 3 - 1)^{2} = 16;\]
\[16 = 16 \Longrightarrow B( - 5; - 3) - на\ \]
\[окружности.\]
\[3)\ C( - 7; - 2):\]
\[( - 7 + 5)^{2} + ( - 2 - 1)^{2} \neq 16;\ \]
\[4 + 9 \neq 16;\]
\[13 \neq 16 \Longrightarrow C( - 7; - 2) - внутри\ \]
\[круга.\]
\[4)\ D(1;5):\]
\[(1 + 5)^{2} + (5 - 1)^{2} \neq 16;\]
\[36 + 16 \neq 16\]
\[52 \neq 16 \Longrightarrow \ D(1;5) - вне\ круга.\]
\[Ответ:а)\ C;б)\ B;в)\ A\ и\ \text{D.}\]
\[\boxed{\mathbf{961.еуроки - ответы\ на\ пятёрку}}\]
\[Доказать:\]
\[для\ любых\ двух\ векторов\]
\[\ \overrightarrow{x}\ и\ \overrightarrow{y}\ \ справедливо\ \]
\[неравенство\ \left| \overrightarrow{x} - \overrightarrow{y} \right| \leq \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|;\]
\[в\ каком\ случае\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|?\]
\[Доказательство.\]
\[Разберем\ четыре\ возможных\ \]
\[варианта.\]
\[1)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ неколлинеарные\ \]
\[векторы,\ тогда\ векторы\ \overrightarrow{x}\ и\ \overrightarrow{y},\ а\]
\[также\ \overrightarrow{x} - \overrightarrow{y},\ будут\ сторонами\ \]
\[одного\ треугольника:\]
\[2)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ коллинеарны\ \]
\[и\ противоположно\ \]
\[направлены:\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[3)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ коллинеарны\ \]
\[и\ сонаправлены:\]
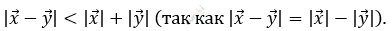
\[4)\ Пусть\ один\ из\ векторов\ \]
\[нулевой:\]
\[\ \left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[Отсюда:\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| \leq \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[Что\ и\ требовалось\ доказать.\]
\[Вопрос:в\ каком\ случае\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|?\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right| \Longrightarrow \ когда\ \]
\[векторы\ \overrightarrow{x} \uparrow \downarrow \overrightarrow{y},\ либо\ \overrightarrow{x} = \overrightarrow{0}\ или\]
\[\ \overrightarrow{y} = \overrightarrow{0}.\ \]
