Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 892
Задание 892
\[\boxed{\mathbf{892.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - трапеция;\]
\[AD \parallel BC;\]
\[\angle A = 90{^\circ}.\]
\[\mathbf{Доказать:}\]
\[S_{\text{ABCD}} = AD \bullet BC.\]
\[\mathbf{Доказательство.}\]
\[1)\ Отметим\ точки\ касания\ \]
\[окружностью\ сторон\ трапеции:\]
\[E,F,G\ и\ \text{H.}\]
\[2)\ Рассмотрим\ \]
\[четырехугольник\ ABFH:\]
\[OH\bot AD\ и\ OF\bot BC\ и\ O \in FH.\]
\[Следовательно:\]
\[ABFH - прямоугольник \Longrightarrow\]
\[FH = AB = 2r = h;\]
\[\Longrightarrow BF = AH = OE = r.\]
\[3)\ Опустим\ высоту\ CK\bot AD;\]
\[CK^{2} = h^{2} = CD^{2} - KD^{2} =\]
\[= CD^{2} - (AD - BC)^{2}.\]
\[4)\ По\ свойству\ описанного\ \]
\[четырехугольника:\]
\[AD + BC = AB + CD.\]
\[5)\ CD = AD + BC - AB =\]
\[= AD + BC - h;\]
\[h^{2} =\]
\[= (AD + BC - h)^{2} - (AD - BC)^{2};\]
\[2h(AD + BC) =\]
\[= (AD + BC)^{2} - (AD - BC)^{2};\]
\[2h(AD + BC) =\]
\[2h(AD + BC) = 4AD \bullet BC\]
\[h(AD + BC) = 2AD \bullet BC.\]
\[6)\ S_{\text{ABCD}} = \frac{h(AD + BC)}{2} =\]
\[= \frac{2AD \bullet BC}{2} = AD \bullet BC.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{892.еуроки - ответы\ на\ пятёрку}}\]
\[Дано:\]
\[⊿ABC;\]
\[A_{1}B_{1}C_{1} - на\ прямых\ \]
\[BC;AC;BA;\]
\[\frac{A_{1}C}{C_{1}B} \cdot \frac{BA_{1}}{A_{1}C} \cdot \frac{CB_{1}}{B_{1}A} = 1.\]
\[Доказать:\]
\[A_{1};B_{1}C_{1} - лежат\ на\ одной\ \]
\[прямой.\]
\[Доказательство.\]
\[Проведем\ прямую\ A_{1}C_{1};\]
\[B_{2} - точка\ ее\ пересечения\ \]
\[с\ прямой\ \text{AC.}\]
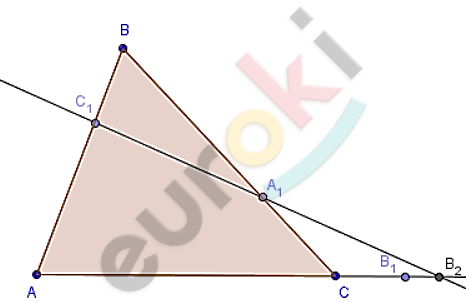
\[По\ теореме\ Менелая:\]
\[\frac{A_{1}C}{C_{1}B} \cdot \frac{BA_{1}}{A_{1}C} \cdot \frac{CB_{1}}{B_{1}A} = 1.\]
\[Тогда:\]
\[\frac{CB_{1}}{B_{1}A} = \frac{CB_{2}}{B_{2}A}.\]
\[Пусть\ CB_{1} = x;\ \ CB_{2} = y;\]
\[AC = b.\]
\[Получаем:\]
\[\frac{x}{b + x} = \frac{y}{b + y}\]
\[x(b + y) = y(b + x)\]
\[x(x - y) = 0\ \ \ \ \ \ \ \ |\ :b\]
\[x = y.\]
\[Из\ аксиомы\ об\ откладывании\ \]
\[отрезка\ следует,\ что\ B_{1}\ \]
\[совпадает\ с\ B_{2}.\]
\[Значит,\ все\ точки\ находятся\ \]
\[на\ одной\ прямой.\]
\[Что\ и\ требовалось\ доказать.\]
