Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 89
Задание 89
\[\boxed{\mathbf{89.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\]
\[\textbf{б)}\]
\(\ \)
\[\textbf{в)}\]
\(\ \)
\[\boxed{\mathbf{89.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
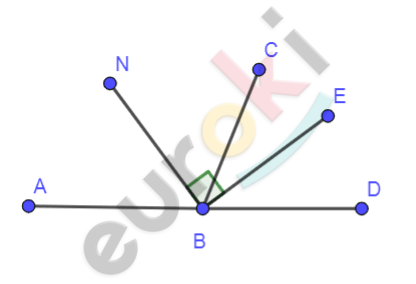
\[Дано:\]
\[\angle\text{EBN} = 90{^\circ}\]
\[\text{BE} - биссектриса\ \angle\text{CBD}\]
\[\text{BN} - биссектриса\ \angle\text{ABC}\]
\[Доказать:\]
\[A,B,D - лежат\ на\ одной\ \]
\[прямой.\ \ \]
\[Доказательство.\]
\[\angle EBN = 90{^\circ};\ \ \]
\[\angle EBN = \angle EBC + \angle\text{CBN.}\]
\[Пусть\ \angle EBC = x;\]
\[\ \angle CBN = 90{^\circ} - x.\]
\[BN - биссектриса\ \angle ABC \Longrightarrow\]
\[\Longrightarrow \angle ABN = \angle NBC = 90{^\circ} - x.\ \]
\[BE - биссектриса\ \angle CBD \Longrightarrow\]
\[\Longrightarrow \angle DBE = \angle EBC = x.\]
\[Получаем:\]
\[\angle ABD = \angle ABC + \angle DBC =\]
\[= 2(90{^\circ} - x) + 2x =\]
\[= 180{^\circ} - 2x + 2x = 180{^\circ}.\]
\[\angle ABD = 180{^\circ} - развернутый.\]
\[Следовательно,\ все\ точки\ этого\ \]
\[угла\ лежат\ на\ одной\ прямой.\]
\[Что\ и\ требовалось\ доказать.\]
