Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 888
Задание 888
\[\boxed{\mathbf{888.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[BH\bot AC;\]
\[\angle ABE = \angle EBC.\]
\[\mathbf{Доказать:}\]
\[\angle OBE = \angle HBE.\]
\[\mathbf{Доказательство.}\]
\[1)\ Пусть\ \angle BCA = \alpha;\ \]
\[\angle ABE = \angle EBC = \beta:\]
\[\angle AOB = 2\alpha.\]
\[2)\ \mathrm{\Delta}ABO - равнобедренный:\]
\[\angle ABO = \frac{1}{2}(180{^\circ} - \angle AOB) =\]
\[= 90{^\circ} - \frac{1}{2}\angle AOB = 90{^\circ} - \alpha.\]
\[3)\ \angle OBE = \angle ABE - \angle ABO =\]
\[= \beta - (90{^\circ} - \alpha) = \alpha + \beta - 90{^\circ};\]
\[\angle HBE = \angle EBC - \angle HBC =\]
\[= \beta - (90{^\circ} - \alpha) = \alpha + \beta - 90{^\circ};\]
\[\angle OBE = \angle HBE.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{888.еуроки - ответы\ на\ пятёрку}}\]
\[Дано:\]
\[a - основание;\]
\[b - боковая\ сторона;\]
\[\angle A - угол\ между\ ними;\]
\[\frac{n}{m} - соотношение\ двух\ других\ \]
\[сторон.\]
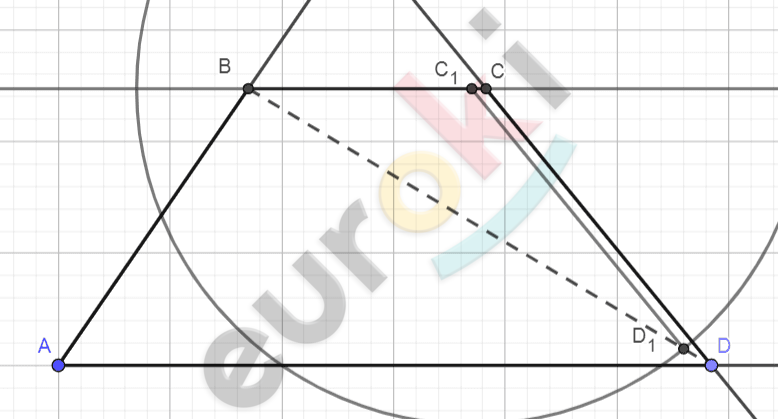
\[Построить:\]
\[трапецию\ \text{ABCD.}\]
\[Построение.\]
\[1)\ На\ сторонах\ угла\ \text{A\ }\]
\[отложим\ отрезки\ AD = a\ и\ \]
\[AB = b.\]
\[2)\ Построим\ отрезок\ BD -\]
\[диагональ\ трапеции.\]
\[3)\ Построим\ прямую\ \]
\[параллельную\ AD,\ отложим\ \]
\[на\ ней\ отрезок\ BC_{1}\ равный\ m.\]
\[4)\ Построим\ окружность\ \]
\[\left( C_{1};n \right),\ на\ пересечении\ \]
\[с\ отрезком\ \text{BD}\ отметим\]
\[\ точку\ D_{1}.\]
\[5)\ Построим\ прямую\ \]
\[параллельную\ C_{1}D_{1}\ через\ \]
\[точку\ D,\ на\ пересечении\]
\[с\ прямой\ BC_{1}\ отметим\ точку\ \text{C.}\]
