Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 824
Задание 824
\[\boxed{\mathbf{824.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
\[\mathbf{Дано:}\]
\(квадраты\) \(AGBF;FBCH;HCDE.\)
\[\mathbf{Найти:}\]
\[\angle BAE + \angle CAE + \angle DAE.\]
\[\mathbf{Решение.}\]
\[1)\ Диагональ\ квадрата\ \]
\[является\ биссектрисой\ угла:\ \]
\[\angle BAE = \angle BAF = 45{^\circ}.\]
\[2)\ Достроим\ чертеж,\ как\ \]
\[показано\ на\ рисунке\]
\[(добавим\ еще\ несколько\ квадратов).\]
\[3)\ Получим\ по\ построению\ \]
\[равнобедренный\ треугольник\ \]
\[\text{KAC},\ с\ основанием\ \text{KC}:\]
\[AH - высота,\ биссектриса\ и\ \]
\[медиана.\]
\[Следовательно:\ \]
\[\angle CAE = \angle CAH = \angle KAH;\]
\[\angle KAD = \angle CAE + \angle DAE.\]
\[3)\ Треугольник\ AKS -\]
\[равнобедренный\ по\ \]
\[построению:\]
\[\angle AKS = 90{^\circ}.\]
\[Углы\ при\ основании\ будут\ \]
\[равны:\]
\[\angle SAK = \angle ASK = 45{^\circ} = \angle BAE.\]
\[4)\ Получаем:\]
\[\angle SAD =\]
\[= \angle SAK + \angle KAH + \angle EAD =\]
\[= \angle BAE + \angle CAE + \angle DAE.\]
\[5)\ \ \angle TAE = 90{^\circ};\ \ \mathrm{\Delta}TAS = \mathrm{\Delta}EAD:\]
\[\angle TAS = \angle EAD.\]
\[6)\ Следовательно:\]
\[\angle SAD =\]
\[= \angle TAE + \angle EAD - \angle TAS = 90{^\circ}.\]
\[Ответ:\ \]
\[\angle BAE + \angle CAE + \angle DAE = 90{^\circ}.\]
\[\boxed{\mathbf{824.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
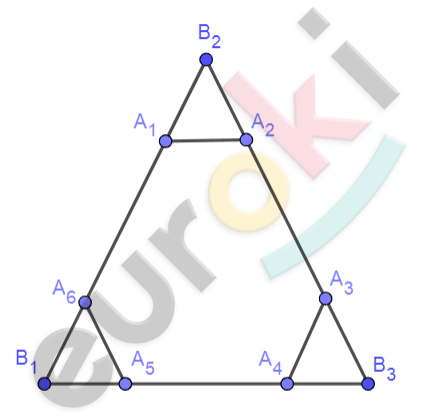
\[A_{1}A_{2}A_{3}A_{4}A_{5}A_{6} - выпуклый\ \]
\[четырехугольник;\]
\[\angle A_{1} = \angle A_{2} = \angle A_{3} = \angle A_{4} =\]
\[= \angle A_{5} = \angle A_{6} = \alpha.\]
\[\mathbf{Доказать:}\]
\[A_{1}A_{2} - A_{4}A_{5} = A_{5}A_{6} - A_{2}A_{3} =\]
\[= A_{3}A_{4} - A_{6}A_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ Допустим:\]
\[A_{1}A_{2} = a_{1};\ \ A_{2}A_{3} = a_{2};\ \ \]
\[A_{3}A_{4} = a_{3};\]
\[A_{4}A_{5} = a_{4};\ \ \ \ A_{5}A_{6} = a_{5};\ \]
\[\ A_{6}A_{1} = a_{6}.\]
\[2)\ Начертим\ продолжение\ \]
\[сторон\ A_{1}A_{6};\ \ A_{2}A_{3};\ \ A_{4}A_{5};\ \ \ \]
\[получим\ \mathrm{\Delta}B_{1}B_{2}B_{3}.\]
\[3)\ 6 \bullet \alpha = 180 \bullet (6 - 2)\]
\[\alpha = \frac{180 \bullet 4}{6} = 120{^\circ}.\]
\[Смежные\ с\ ними\ углы\ будут\ \]
\[равны:\]
\[\angle B_{1} = \angle B_{2} = \angle B_{3} = 60{^\circ}.\]
\[\mathrm{\Delta}B_{3}A_{6}A_{5};\ \mathrm{\Delta}B_{1}A_{1}A_{2};\ \ \mathrm{\Delta}B_{2}A_{4}A_{3} -\]
\[равносторонние:\]
\[B_{1}B_{2} = B_{2}B_{3} = B_{1}B_{3}\text{.\ \ }\]
\[Значит:\]
\[a_{1} + a_{2} + a_{3} = a_{3} + a_{4} + a_{5} =\]
\[= a_{5} + a_{6} + a_{1}.\]
\[4)\ Продолжим:\]
\[a_{1} + a_{2} = a_{4} + a_{5};\ \ \]
\[\text{\ \ }a_{1} - a_{4} = a_{5} - a_{2};\]
\[a_{3} + a_{4} = a_{6} + a_{1};\ \]
\[\text{\ \ }a_{1} - a_{4} = a_{3} - a_{6};\]
\[a_{1} - a_{4} = a_{5} - a_{2} = a_{3} - a_{6}.\]
\[Отсюда:\]
\[A_{1}A_{2} - A_{4}A_{5} = A_{5}A_{6} - A_{2}A_{3} =\]
\[= A_{3}A_{4} - A_{6}A_{1}.\]
\[Что\ и\ требовалось\ доказать.\]
