Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 819
Задание 819
\[\boxed{\mathbf{819.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
\[\mathbf{Дано:}\]
\[a - прямая;\]
\[C \in a.\]
\[\mathbf{Найти:}\]
\[множество\ середин\ всех\ \]
\[отрезков,\ соединяющих\ C\ со\ \]
\[всеми\ точками\ прямой\ \text{a.}\]
\[\mathbf{Решение.}\]
\[1)\ Начертим\ из\ ( \bullet )\text{C\ }\]
\[перпендикуляр\ к\ прямой\ \text{a\ }так,\ \]
\[чтобы\ \ ( \bullet )\text{\ A\ }принадлежала\ \text{a.}\]
\[2)\ Серединой\ отрезка\ \text{AC\ }\]
\[будет\ ( \bullet )A_{1}:\]
\[AA_{1} = A_{1}C = \frac{1}{2}\text{AC.}\]
\[3)\ Через\ точку\ A_{1}\ проведем\ \]
\[прямую\ b,\ параллельную\ \]
\[прямой\ \text{a.}\]
\[4)\ На\ прямой\ \text{a\ }отметим\ \]
\[произвольную\ ( \bullet )\text{X.}\]
\[Надо\ доказать,\ что\ X_{1} \in b -\]
\[середина\ отрезка\ \text{CX.}\]
\[5)\ A_{1}X_{1} - средняя\ линия\ \mathrm{\Delta}ACX\ \]
\[(по\ построению):\ \]
\[\ A_{1}X_{1} \parallel AX \Longrightarrow \ A_{1}X_{1} \parallel a.\]
\[6)\ Известно,\ что\ через\ точку,\ \]
\[не\ лежащую\ на\ прямой,\ можно\ \]
\[провести\ только\ одну\ прямую,\ \]
\[параллельную\ данной.\ \]
\[Следовательно:\]
\[A_{1}X_{1} \subset b;\ \ \ X_{1} \in b.\]
\[Ответ:множеством\ середин\ \]
\[всех\ отрезков\ является\ прямая,\ \]
\[параллельная\ прямой\ \text{a\ }и\ \]
\[лежащая\ между\ точкой\ и\ этой\]
\[прямой\ на\ половине\ \]
\[расстояния\ между\ ними.\]
\[\boxed{\mathbf{819.еуроки - ответы\ на\ пятёрку}}\]
\[Дано:\]
\[ABCD - четырехугольник;\]
\[M;N;P;Q - точки\ касания\ \]
\[окружности\ со\ сторонами.\]
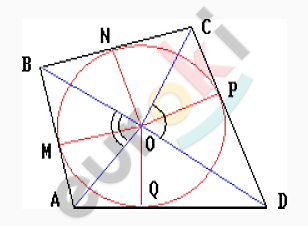
\[Доказать:\]
\[\angle AOD + \angle BOC =\]
\[= \angle AOB + \angle COD.\]
\[Доказательство.\]
\[Центр\ окружности,\ вписанной\ \]
\[в\ четырехугольник - это\ \]
\[точка\ пересечения\ биссектрис\ \]
\[внутренних\ углов\ этого\ \]
\[треугольника.\]
\[Пусть\ \angle MON = 2\alpha;\ \ \]
\[\angle NOP = 2\beta;\ \angle POQ = 2\gamma;\ \]
\[\angle QOM = 2\varphi.\]
\[Тогда:\]
\[\angle AOB = \alpha + \varphi;\]
\[\angle COD = \beta + \gamma;\]
\[\angle AOB + \angle COD =\]
\[= \alpha + \beta + \gamma + \varphi = \frac{1}{2} \cdot 360{^\circ} =\]
\[= 180{^\circ}.\]
\[Аналогично\ получаем:\]
\[\angle AOD + \angle BOC = 180{^\circ}.\]
\[Следовательно:\]
\[\angle AOD + \angle BOC =\]
\[= \angle AOB + \angle COD.\]
\[Что\ и\ требовалось\ доказать.\]
