Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 800
Задание 800
\[\boxed{\mathbf{800.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:}\]
\[\textbf{а)}\ \overrightarrow{m} \nearrow \nearrow \overrightarrow{n};\ \]
\[\textbf{б)}\ \overrightarrow{m} \nearrow \nearrow \overrightarrow{n}\ и\ \ \left| \overrightarrow{m} \right| \geq \overrightarrow{n}.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ \left| \overrightarrow{m} + \overrightarrow{n} \right| = \left| \overrightarrow{m} \right| + \left| \overrightarrow{n} \right|;\]
\[\textbf{б)}\ \left| \overrightarrow{m} + \overrightarrow{n} \right| = \left| \overrightarrow{m} \right| - \left| \overrightarrow{n} \right|.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\ \left| \overrightarrow{\text{AB}} \right| + \left| \overrightarrow{\text{BC}} \right| = \left| \overrightarrow{\text{AC}} \right|:\]
\[\ \left| \overrightarrow{m} + \overrightarrow{n} \right| = \left| \overrightarrow{m} \right| + \left| \overrightarrow{n} \right|.\]
\[\textbf{б)}\ AB = AC + BC:\]
\[\overrightarrow{\text{AC}} = \left| \overrightarrow{m} \right| + \left| \overrightarrow{n} \right|\ \]
\[\left| \overrightarrow{\text{AC}} \right| = \left| \overrightarrow{\text{AB}} \right| - \left| \overrightarrow{\text{BC}} \right|.\]
\[Следовательно:\]
\[\left| \overrightarrow{m} \right| + \left| \overrightarrow{n} \right| = \left| \overrightarrow{m} \right| - \left| \overrightarrow{n} \right|\]
\[\boxed{\mathbf{800.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[окружность\ (O;r);\]
\[A,B,C,D \in (O;r);\]
\[\cup AB = \cup CD.\]
\[\mathbf{Доказать:}\]
\[AB = CD.\]
\[\mathbf{Доказательство.}\]
\[1)\ \angle AOB = \cup AB\ и\ \angle COD =\]
\[= \cup CD\ (как\ центральные\ углы);\]
\[\cup AB = \cup CD.\]
\[Значит:\ \]
\[\angle AOB = \angle COD.\]
\[2)\ \mathrm{\Delta}AOB = \mathrm{\Delta}COD - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[AO = OB = OC = OD = r;\ \]
\[\angle AOB = \angle COD.\]
\[Отсюда:\ \]
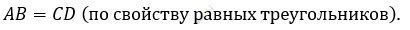
\[Что\ и\ требовалось\ доказать.\]
