Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 789
Задание 789
\[\boxed{\mathbf{789.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[\text{AB}B_{1}A_{2};BCC_{1}B_{2}\ и\ \]
\[\text{AC}C_{2}A_{1} - параллелограммы.\]
\[\mathbf{Доказать:}\]
\[существует\ треугольник,\ \]
\[стороны\ которого\ \]
\[параллельны\ и\ равны\]
\[\overrightarrow{\ A_{1}A_{2}};\overrightarrow{B_{1}B_{2}}\ и\ \overrightarrow{C_{1}C_{2}}.\]
\[\mathbf{Доказательство.}\]
\[1)\ Если\ треугольник\ \]
\[существует,\ то\ сумма\ векторов\ \]
\[будет\ равна:\ \]
\[\overrightarrow{A_{1}A_{2}} + \overrightarrow{B_{1}B_{2}} + \overrightarrow{C_{1}C_{2}} = \overrightarrow{0}.\]
\[2)\ По\ определению\ \]
\[параллелипеда:\]
\[\ \overrightarrow{AA_{2}} = \overrightarrow{BB_{1}};\]
\[\overrightarrow{BB_{2}} = \overrightarrow{CC_{1}};\]
\[\overrightarrow{AA_{1}} = \overrightarrow{CC_{2}}.\]
\[3)\ По\ правилу\ треугольника:\ \]
\[\overrightarrow{A_{1}A_{2}} = \overrightarrow{A_{1}A} + \overrightarrow{AA_{2}};\]
\[\overrightarrow{B_{1}B_{2}} = \overrightarrow{B_{1}B} + \overrightarrow{BB_{2}};\]
\[\overrightarrow{C_{1}C_{2}} = \overrightarrow{C_{1}C} + \overrightarrow{CC_{2}}\text{.\ }\]
\[4)\ Складываем\ полученные\ \]
\[равенства:\]
\[\overrightarrow{A_{1}A_{2}} + \overrightarrow{B_{1}B_{2}} + \overrightarrow{C_{1}C_{2}} =\]
\[Следовательно,\ существует\ \]
\[треугольник,\ у\ которого\ \]
\[стороны\ равны\ и\ параллельны\]
\[\ \overrightarrow{A_{1}A_{2}};\ \overrightarrow{B_{1}B_{2}};\ \ \overrightarrow{C_{1}C_{2}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{789.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
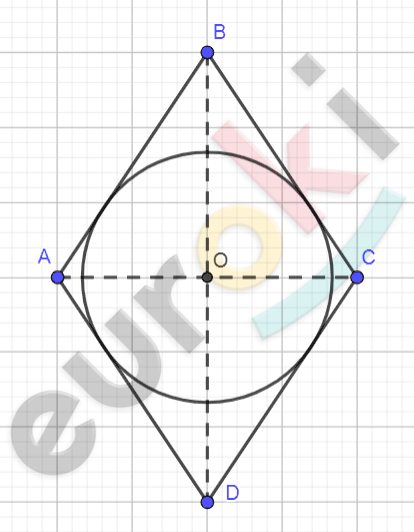
\[\mathbf{Доказать:}\]
\[\mathbf{в\ любой\ ромб\ можно\ вписать\ }\]
\[\mathbf{окружность}\mathbf{.}\]
\[\mathbf{Доказательство.}\]
\[1)\ ABCD - ромб:\]
\[AB = BC = CD = AD\ \]
\[(по\ определению\ ромба).\]
\[2)\ Для\ того,\ чтобы\ \]
\[в\ четырехугольник\ можно\ \]
\[было\ вписать\ окружность,\ \]
\[должно\ выполняться\]
\[условие:\]
\[AB + CD = BC + AD\ \]
\[3)\ AB + CD = BC + AD -\]
\[условие\ выполняется.\]
\[Следовательно,\ в\ любой\ ромб\ \]
\[можно\ вписать\ окружность.\]
\[Что\ и\ требовалось\ доказать.\]
