Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 787
Задание 787
\[\boxed{\mathbf{787.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}DEF;\]
\[EG - медиана;\]
\[\text{EO} = \text{OG};\]
\[\overrightarrow{a} = \overrightarrow{\text{ED}};\ \]
\[\overrightarrow{b} = \overrightarrow{\text{EF}}.\]
\[Выразить:\]
\(\overrightarrow{\text{DO}}\ через\ \overrightarrow{a}\text{\ \ }и\ \overrightarrow{b}\).
\[\mathbf{Решение.}\]
\[1)\ \overrightarrow{\text{ED}} + \overrightarrow{\text{DF}} = \overrightarrow{\text{EF}}\]
\[\overrightarrow{\text{DF}} = \overrightarrow{\text{EF}} - \overrightarrow{\text{ED}} = \overrightarrow{b} - \overrightarrow{a}.\]
\[2)\ \overrightarrow{\text{GE}} = \overrightarrow{\text{GD}} + \overrightarrow{\text{DE}} =\]
\[= - \frac{1}{2}\overrightarrow{\text{DF}} - \overrightarrow{\text{ED}} =\]
\[= - \frac{1}{2} \bullet \left( \overrightarrow{b} - \overrightarrow{a} \right) - \overrightarrow{a} =\]
\[= - \frac{1}{2}\overrightarrow{b} + \frac{1}{2}\overrightarrow{a} - \overrightarrow{a} = - \frac{1}{2}\overrightarrow{b} - \frac{1}{2}\overrightarrow{a}.\]
\[3)\ \overrightarrow{\text{DO}} = \overrightarrow{\text{DG}} + \overrightarrow{\text{GO}} =\]
\[= \frac{1}{2}\overrightarrow{\text{DF}} + \frac{1}{2}\overrightarrow{\text{GE}} =\]
\[= \frac{1}{2} \bullet \left( \overrightarrow{b} - \overrightarrow{a} \right) + \frac{1}{2} \bullet \left( - \frac{1}{2}\overrightarrow{b} - \frac{1}{2}\overrightarrow{a} \right) =\]
\[= \frac{1}{2}\overrightarrow{b} - \frac{1}{2}\overrightarrow{a} - \frac{1}{4}\overrightarrow{b} - \frac{1}{4}\overrightarrow{a} =\]
\[= \frac{1}{4}\overrightarrow{b} - \frac{3}{4}\ \overrightarrow{a}.\]
\[Ответ:\ \overrightarrow{\text{DO}} = \frac{1}{4}\overrightarrow{b} - \frac{3}{4}\ \overrightarrow{a}.\]
\[\boxed{\mathbf{787.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - четырехугольник;\]
\[четыреугольн;\]
\[r = 5\ см;\]
\[AB + CD = 12.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABCD}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ В\ \text{ABCD\ }можно\ вписать\ \]
\[окружность:\]
\[AB + CD = BC + AD\ \]
\[(по\ свойству\ вписанной\ \]
\[окружности\ в\ \ \]
\[четырехугольник).\]
\[2)\ S_{\text{ABCD}} =\]
\[= S_{\text{AOB}} + S_{\text{BCO}} + S_{\text{COD}} + S_{\text{AOD}};\]
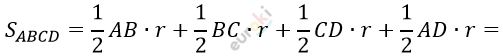
\[= \frac{1}{2}r(AB + BC + CD + AD) =\]
\[= \frac{1}{2} \bullet 5(12 + 12) = \frac{1}{2} \bullet 5 \bullet 24 =\]
\[= 60\ см^{2}.\]
\[Ответ:S_{\text{ABCD}} = 60\ см^{2}.\ \]
