Решебник по геометрии 7 класс Атанасян ФГОС Задание 78

 

\[\boxed{\mathbf{78.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[Дано:\]

\[AB = 36\ см\]

\[FG = 30\ см\]

\[Найти:\]

\[HI - ?\]

\[Решение.\]

\[1)\ Надо\ найти\ длину\ \]

\[отрезка\ CE:\]

\[CE = AB - (AC + EB)\]

\[AC + EB =\]

\[= (AF + GB) + (FC + EG)\]

\[AF + GB = AB - FG =\]

\[= 36\ см - 30\ см = 6\ см.\]

\[2)\ Отрезки\ FC\ и\ \text{EG\ }являются\ \]

\[половинами\ отрезков\ \text{AC\ }и\ EB:\ \]

\[FC + EG = AF + GB = 6\ см.\]

\[AC + EB = 6\ см + 6\ см = 12\ см.\]

\[CE = 36\ см - 12\ см = 24\ см.\]

\[3)\ Точки\ \text{H\ }и\ \text{I\ }являются\ \]

\[серединами\ отрезков\ \text{CD\ }и\ DE:\ \]

\[CH + IE = HD + DI\]

\(\text{HI} = \text{HD} + \text{DI} = \text{CE}\ :2 =\)

\[= 24\ см\ :\ 2 = 12\ см.\]

\[Ответ:12\ см.\]

\[\boxed{\mathbf{78.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\ \]

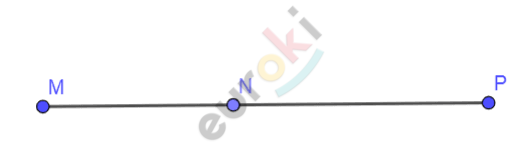
\[Дано:\]

\[MP = 24\ см\]

\[NM = 2NP\]

\[Найти:\]

\[\textbf{а)}\ NP\]

\[\textbf{б)}\ NM\]

\[Решение.\]

\[Пусть\ NP = x,\ тогда\ NM = 2x,\]

\[MP = NP + NM.\]

\[Составим\ уравнение:\]

\[24 = x + 2x\]

\[3x = 24\]

\[x = \frac{24}{3}\]

\[x = 8\ см.\]

\[\textbf{а)}\ NP = 8\ см.\]

\[\textbf{б)}\ NM = 2 \bullet 8\ см = 16\ см.\]

\[Ответ:а)\ 8\ см;\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ 16\ см.\]