Решебник по геометрии 7 класс Атанасян ФГОС Задание 778

 

\[\boxed{\mathbf{778.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Построим\ вектроры\ }\overrightarrow{a},\ \overrightarrow{b}\ и\ \overrightarrow{c}.\]

\[\textbf{а)}\ 2\overrightarrow{a} + 3\overrightarrow{b} - 4\overrightarrow{c};\]

\[\textbf{б)}\frac{1}{2}\overrightarrow{a} - \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\text{\ .}\]

\[\boxed{\mathbf{778.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

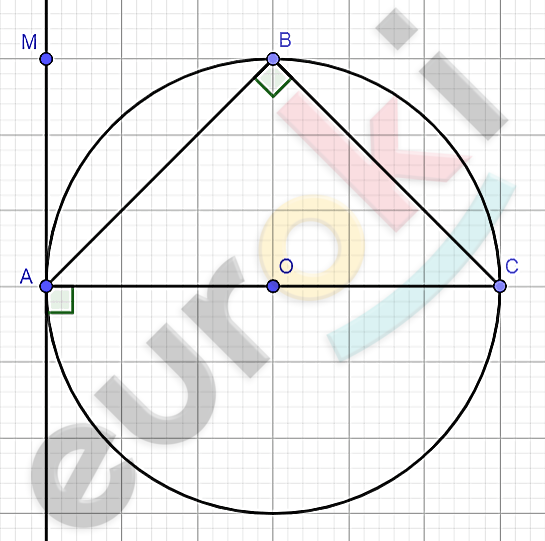
\[окружность\ (O;r);\]

\[AC - диаметр;\]

\[AB - хорда;\]

\[AM - касательная;\]

\[\angle MAB < 90{^\circ}.\]

\[\mathbf{Доказать:}\]

\[\angle MAB = \angle ACB.\]

\[\mathbf{Доказательство.}\]

\[1)\ По\ теореме\ о\ вписанном\ \]

\[угле:\]

\[\angle ABC = \frac{1}{2} \cup AC = \frac{1}{2} \bullet 180{^\circ} = 90{^\circ}.\]

\[2)\ По\ свойству\ \]

\[прямоугольного\ треугольника:\]

\[\angle BCA = 90{^\circ} - \angle BAC.\]

\[3)\ AM - касательная \Longrightarrow\]

\[\Longrightarrow AC\bot AM:\]

\[\angle MAB = 90{^\circ} - \angle BAC.\]

\[4)\ \angle ACB = 90{^\circ} - \angle BAC\ и\ \]

\[\angle MAB = 90{^\circ} - \angle BAC.\]

\[Следовательно:\]

\[\angle ACB = \angle MAB.\]

\[Что\ и\ требовалось\ доказать.\]