Решебник по геометрии 7 класс Атанасян ФГОС Задание 777

 

\[\boxed{\mathbf{777.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Построим\ вектроры\ }\overrightarrow{p},\overrightarrow{q}.\]

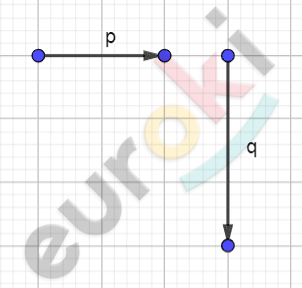
\[1)\ \overrightarrow{m} = 2\overrightarrow{p} - \frac{1}{2}\overrightarrow{q};\]

\[2)\ \overrightarrow{n} = \overrightarrow{p} + 3\overrightarrow{q};\]

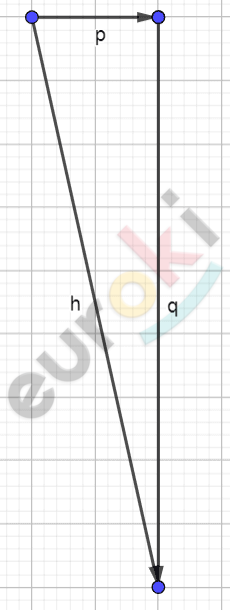
\[3)\ \overrightarrow{l} = - 2\overrightarrow{p} - \frac{1}{2}\overrightarrow{q};\]

\[4)\ \overrightarrow{s} = \frac{2}{3}\overrightarrow{q} - \overrightarrow{p}.\]

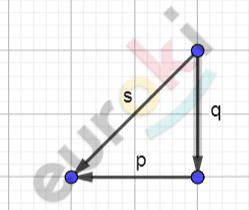
\[\boxed{\mathbf{777.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

\[\mathbf{Дано:}\]

\[окружность\ (O,\ r);\ \]

\[AB;CD - хорды;\]

\[AB \cap CD = E;\]

\[\cup AD = 54{^\circ};\]

\[\cup BC = 70{^\circ}.\]

\[\mathbf{Найти:}\]

\[\angle BEC - ?\]

\[\mathbf{Решение.}\]

\[1)\ По\ теореме\ о\ вписанном\ \]

\[угле:\]

\[\angle BAC = \frac{1}{2} \cup BC = \frac{1}{2} \bullet 70{^\circ} = 35{^\circ}\ ;\]

\[\angle DCA = \frac{1}{2} \cup AD = \frac{1}{2} \bullet 54{^\circ} = 27{^\circ}.\]

\[3)\ По\ теореме\ о\ сумме\ углов\ \]

\[в\ треугольнике:\]

\[\angle AEC = 180{^\circ} - 35{^\circ} - 27{^\circ} =\]

\[= 118{^\circ}.\]

\[4)\ \angle BEC = 180{^\circ} - 118{^\circ} = 62{^\circ}\ \]

\[(как\ смежные).\]

\[Ответ:\ \angle BEC = 62{^\circ}.\]