Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 762
Задание 762
\[\boxed{\mathbf{762.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC - равносторонний;\]
\[AB = BC = AC = a.\]
\[Найти:\]
\[\textbf{а)}\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} \right|;\ \]
\[\textbf{б)}\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{AC}} \right|;\ \]
\[\textbf{в)}\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{CB}} \right|;\ \]
\[\textbf{г)}\left| \overrightarrow{\text{BA}} - \overrightarrow{\text{BC}} \right|;\ \]
\[\textbf{д)}\left| \overrightarrow{\text{AB}} - \overrightarrow{\text{AC}} \right|\text{.\ }\]
\[Решение.\]
\[\textbf{а)}\ \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} = \overrightarrow{\text{AC}} =\]
\[= a\ (по\ правилу\ треугольника).\]
\[\left| \overrightarrow{\text{AD}} \right| = 2AO;\]
\[AO = \sqrt{a^{2} - \left( \frac{a}{2} \right)^{2}} = \sqrt{\frac{3a^{2}}{4}} =\]
\[= \frac{a\sqrt{3}}{2}\]
\[\left| \overrightarrow{\text{AD}} \right| = 2 \bullet \frac{a\sqrt{3}}{2} = a\sqrt{3}.\]
\[\textbf{в)}\ \overrightarrow{\text{AB}} + \overrightarrow{\text{CB}} = \overrightarrow{\text{CD}} + \overrightarrow{\text{DE}} =\]
\[= \overrightarrow{\text{CE}}\ (DE \parallel BC;DE = BC):\]
\[CDEB - ромб\ \]
\[(по\ построению) \Longrightarrow CE = AD.\]
\[Следовательно:\]
\[\left| \overrightarrow{\text{CE}} \right| = a\sqrt{3}.\]
\[\textbf{г)}\ \overrightarrow{\text{BA}} - \overrightarrow{\text{BC}} = \overrightarrow{\text{CA}} =\]
\[= a\ (по\ правилу\ треугольника).\]
\[\textbf{д)}\ \overrightarrow{\text{AB}} - \overrightarrow{\text{AC}} = \overrightarrow{\text{CB}} =\]
\[= a\ (по\ правилу\ треугольника).\]
\[Ответ:а)\ a;б)\ a\sqrt{3};в)\ a\sqrt{3};\]
\[\textbf{г)}\ a;д)\ \text{a.}\]
\[\boxed{\mathbf{762.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathbf{Построить:}\]
\[хорду\ AB,\ так\ чтобы\ \]
\[\textbf{а)}\ \angle AOB = 60{^\circ};\]
\[\textbf{б)}\ \angle AOB = 90{^\circ};\]
\[\textbf{в)}\ \angle AOB = 120{^\circ};\]
\[\textbf{г)}\ \angle AOB = 180{^\circ}.\]
\[Построение.\]
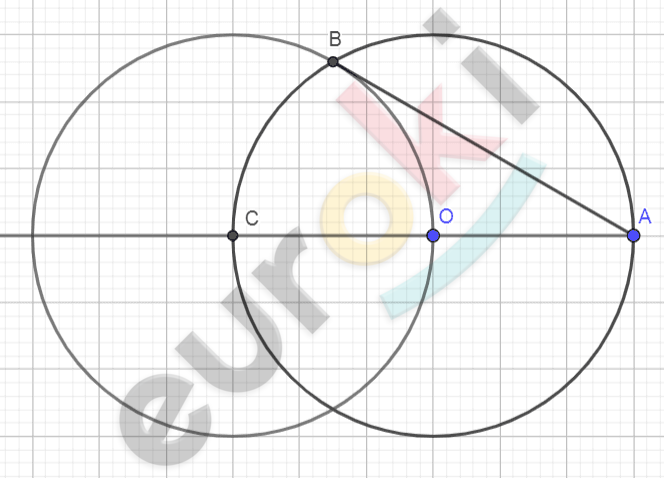
\[\textbf{а)}\ Построим\ окружность\ \]
\[(A;AO);\ отметим\ одну\ из\ точек\ \]
\[пересечения\ окружностей\ \]
\[точкой\ B.\]
\[\textbf{б)}\ Через\ точку\ \text{O\ }построим\ \]
\[прямую\ параллельную\ OA,\ \]
\[на\ пересечении\ данной\ прямой\ \]
\[и\ окружности\ отметим\ точку\ B.\]
\[\textbf{в)}\ Построим\ луч\ AO,\ \]
\[на\ пересечении\ луча\ \]
\[с\ окружностью\ отметим\ точку\]
\[C,\ построим\ окружность\ \]
\[(C;AO)\text{.\ }\]
\[На\ пересечении\ окружностей\ \]
\[отметим\ точку\ \text{B.}\]
\[\textbf{г)}\ Построим\ луч\ AO,\ \]
\[на\ пересечении\ луча\ \]
\[с\ окружностью\ отметим\ \]
\[точку\ \text{B.}\]
