Решебник по геометрии 7 класс Атанасян ФГОС Задание 724

 

\[\boxed{\mathbf{724.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Решение\ задачи\ в\ учебнике.}\]

\[\boxed{\mathbf{724.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

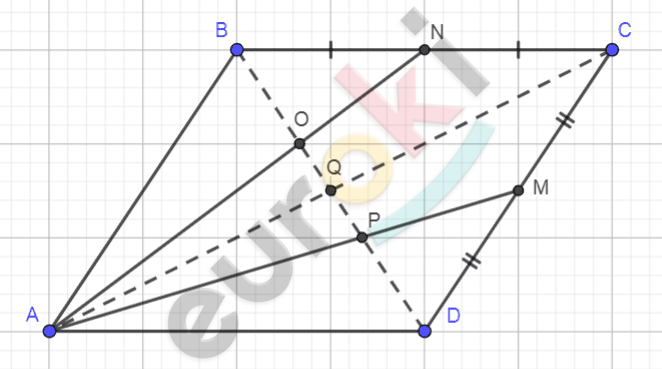
\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[BN = NC;\]

\[CM = MD;\]

\[N \in BC;\]

\[M \in CD;\]

\[AN \cap BD = O;\]

\[AM \cap BD = P.\]

\[\mathbf{Доказать:}\]

\[BO = OP = PD.\]

\[\mathbf{Доказательство.}\]

\[1)\ Рассмотрим\ \mathrm{\Delta}ABC:\]

\[\text{AN\ }и\ BQ - медианы \Longrightarrow\]

\[\Longrightarrow BO\ :OQ = 2\ :1\ \]

\[(по\ свойству\ медиан).\]

\[2)\ Рассмотрим\ \mathrm{\Delta}ACD:\]

\[\text{AM\ }и\ DQ - медианы \Longrightarrow\]

\[\ DP\ :PQ = 2\ :1\ \]

\[(по\ свойству\ медиан).\]

\[3)\ ABCD - параллелограмм:\ \]

\[4)\ BO + OQ = QP + PD.\]

\[5)\ BO\ :OQ = 2\ :1:\]

\[\ BO = \frac{2}{3}BQ;\]

\[BQ = QD = \frac{1}{2}\text{BD.}\]

\[Следовательно:\ \]

\[BO = \frac{\text{BD}}{3}.\]

\[6)\ DP\ :PQ = 2\ :1:\]

\[DP = \frac{2}{3}PQ;\]

\[\ BQ = QD = \frac{1}{2}\text{BD.}\]

\[Следовательно:\ \]

\[DP = \frac{\text{BD}}{3}.\]

\[7)\ OP = BD - BO - DP =\]

\[= BD - \frac{\text{BD}}{3} - \frac{\text{BD}}{3} = \frac{\text{BD}}{3};\]

\[BO = OP = PD.\]

\[Что\ и\ требовалось\ доказать.\]