Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 719
Задание 719
\[\boxed{\mathbf{719.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[Окружность\ (O;r);\]
\[AC,AE - секущие.\]
\[\mathbf{Доказать:}\]
\[\angle CAE = \frac{1}{2}( \cup CE - \cup BD).\]
\[\mathbf{Доказательство.}\]
\[1)\ По\ теореме\ о\ сумме\ углов\ в\ \]
\[треугольнике\ (\mathrm{\Delta}ACD):\ \]
\[\angle A = 180{^\circ} - (\angle C + \angle D).\]
\[2)\ \angle D = 180{^\circ} - \angle CDE\ \]
\[(как\ смежные).\]
\[3)\ \angle CDE = \frac{1}{2} \cup CE\ \]
\[(как\ вписанный\ угол):\ \]
\[\angle D = 180{^\circ} - \frac{1}{2} \cup CE.\]
\[4)\ \angle C = \frac{1}{2} \cup BD\ \]
\[(как\ вписанный\ угол).\]
\[4)\ \angle CAE =\]
\[= 180{^\circ} - \left( \frac{1}{2}BD + 180{^\circ} - \frac{1}{2} \cup CE \right) =\]
\[= 180{^\circ} - \frac{1}{2} \cup BD - 180{^\circ} + \frac{1}{2} \cup CE =\]
\[= \frac{1}{2} \cup CE - \frac{1}{2} \cup BD =\]
\[= \frac{1}{2}( \cup CE - \cup BD).\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{719.еуроки - ответы\ на\ пятёрку}}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
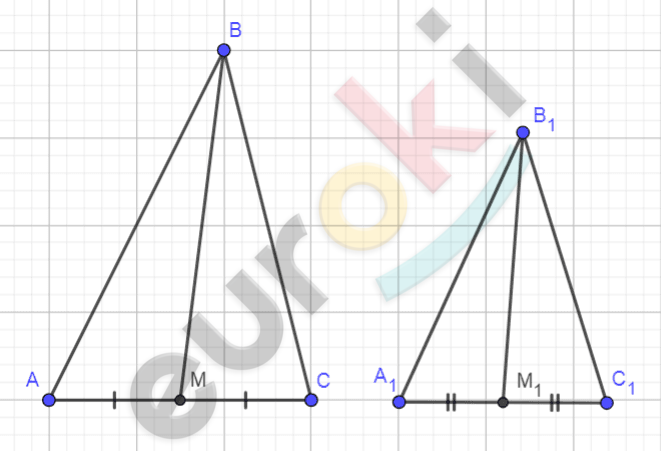
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\ \mathrm{\Delta}A_{1}B_{1}C_{1};\]
\[BM;\ B_{1}M_{1} - медианы;\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{AC}}{A_{1}C_{1}} = \frac{\text{BM}}{B_{1}M_{1}}.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}ABM\sim\mathrm{\Delta}A_{1}B_{1}M_{1} - по\ трем\ \]
\[сторонам:\]
\[AM = \frac{1}{2}\text{AC\ }\]
\[(так\ как\ BM - медиана);\ \ \]
\[A_{1}M_{1} = \frac{1}{2}A_{1}C_{1}\ \]
\[\left( так\ как\ B_{1}M_{1} - медиана \right);\]
\[\frac{\text{AC}}{A_{1}C_{1}} = \frac{\text{BM}}{B_{1}M_{1}}.\]
\[Отсюда:\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{BM}}{B_{1}M_{1}} = \frac{\text{AM}}{A_{1}M_{1}} = k\]
\[Значит:\ \]
\[\angle A = \angle A_{1}.\]
\[2)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1} - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[\angle A = \angle A_{1};\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{AC}}{A_{1}C_{1}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\ \mathrm{\Delta}A_{1}B_{1}C_{1};\]
\[BM;\ \ B_{1}M_{1} - высоты;\]
\[\frac{\text{AC}}{A_{1}C_{1}} = \frac{\text{BH}}{B_{1}H_{1}};\]
\[\angle A = \angle A_{1}.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}ABH\sim\mathrm{\Delta}A_{1}B_{1}H_{1}\ \]
\[(по\ двум\ углам):\]
\[\angle BHA = \angle B_{1}H_{1}A_{1} = 90{^\circ};\ \]
\[\angle A = \angle A_{1}\ (по\ условию).\]
\[Отсюда:\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{BH}}{B_{1}H_{1}} = \frac{\text{AH}}{A_{1}H_{1}} = k.\]
\[2)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1} - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[\angle A = \angle A_{1};\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{AC}}{A_{1}C_{1}}\text{.\ }\]
\[Что\ и\ требовалось\ доказать.\]
