Решебник по геометрии 7 класс Атанасян ФГОС Задание 687

 

\[\boxed{\mathbf{687.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\ \]

\[Построить:\]

\[точку\ M,\ равноудаленную\ \]

\[от\ \text{A\ }и\ \text{B.}\]

\[Построение.\]

\[1)\ Построим\ отрезок\ \text{AB.}\]

\[2)\ Построим\ серединный\ \]

\[перпендикуляр\ к\ отрезку\ \text{AB.}\]

\[3)\ На\ пересечении\ серединного\ \]

\[перпендикуляра\ и\ прямой\ a\]

\[отметим\ точку\ M.\]

\[\boxed{\mathbf{687.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

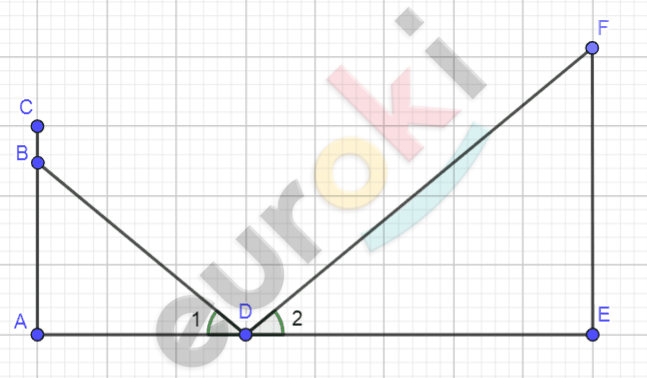
\[\mathbf{Дано:}\]

\[AC = 165\ см;\]

\[BC = 12\ см;\]

\[AD = 120\ см;\]

\[DE = 4,8\ м;\]

\[\angle 1 = \angle 2.\]

\[\mathbf{Найти:}\]

\[FE - ?\]

\[\mathbf{Решение.}\]

\[1)\ \mathrm{\Delta}ABD\sim\mathrm{\Delta}DFE\ \]

\[(по\ двум\ углам):\]

\[\angle A = \angle E = 90{^\circ}\ (по\ условию);\]

\[\angle 1 = \angle 2\ (по\ условию).\]

\[Отсюда:\]

\[\frac{\text{AB}}{\text{FE}} = \frac{\text{AD}}{\text{DE}} = \frac{\text{BD}}{\text{DF}} = k.\]

\[2)\ AB = AC - BC = 165 - 12 =\]

\[= 153\ см.\]

\[3)\ \frac{153}{\text{FE}} = \frac{120}{480}\]

\[\frac{153}{\text{FE}} = \frac{1}{4}\]

\[FE = 153 \bullet 4 = 612\ см.\]

\[Ответ:FE = 612\ см.\]