Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 662
Задание 662
\[\boxed{\mathbf{662.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[окружность\ (O,\ r);\ \]
\[AB;CD - хорды;\]
\[AB \cap CD = E;\]
\[\cup AD = 54{^\circ};\]
\[\cup BC = 70{^\circ}.\]
\[\mathbf{Найти:}\]
\[\angle BEC - ?\]
\[\mathbf{Решение.}\]
\[1)\ По\ теореме\ о\ вписанном\ \]
\[угле:\]
\[\angle BAC = \frac{1}{2} \cup BC = \frac{1}{2} \bullet 70{^\circ} = 35{^\circ}\ ;\]
\[\angle DCA = \frac{1}{2} \cup AD = \frac{1}{2} \bullet 54{^\circ} = 27{^\circ}.\]
\[3)\ По\ теореме\ о\ сумме\ углов\ \]
\[в\ треугольнике:\]
\[\angle AEC = 180{^\circ} - 35{^\circ} - 27{^\circ} =\]
\[= 118{^\circ}.\]
\[4)\ \angle BEC = 180{^\circ} - 118{^\circ} =\]
\[= 62{^\circ}\ (как\ смежные).\]
\[Ответ:\ \angle BEC = 62{^\circ}.\]
\[\boxed{\mathbf{662.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
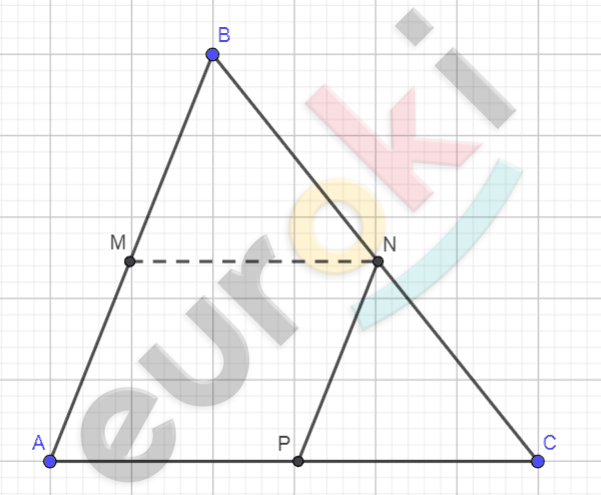
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[M \in AB;N \in BC;\]
\[P \in AC;MN \parallel AC;\]
\[NP \parallel AB;\]
\[\textbf{а)}\ AB = 10\ см;\]
\[AC = 15\ см;\]
\[PN\ :MN = 2\ :3;\]
\[\textbf{б)}\ AM = AP;\]
\[AB = a;\]
\[AC = b.\]
\[\mathbf{Найти:}\]
\[MN - ?;AM - ?;\]
\[AP - ?;PN - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\]
\[1)\ AM \parallel NP,\ MN \parallel AP:\]
\[AMNP - параллелограмм\ \]
\[(по\ определению);\]
\[MN = AP\ и\ AM = NP\ \]
\[(по\ свойству).\]
\[2)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}MBN\ \]
\[(по\ двум\ углам):\]
\[\angle B - общий;\]
\[\angle BMN = \angle BAC\ \]
\[(как\ соответственные).\]
\[3)\ Пусть\ PN = 2x;\ \ \ MN = 3x:\]
\[\frac{10}{10 - 2x} = \frac{15}{3x}\]
\[\frac{5}{5 - x} = \frac{5}{x}\]
\[5 - x = x\]
\[2x = 5.\]
\[x = 2,5\ (см)\text{.\ \ }\]
\(\ PN = 2 \bullet 2,5 = 5\ см.\)
\[MN = 3 \bullet 2,5 = 7,5\ см.\]
\[\textbf{б)}\ \]
\[1)\ AM \parallel NP,\ MN \parallel AP:\]
\[AMNP - параллелограмм\ \]
\[(по\ определению);\]
\[AM = AP.\]
\[Значит:\]
\[AMNP - ромб\ \]
\[(по\ определению).\]
\[2)\ Пусть\ AM = x:\]
\[\frac{\text{AB}}{\text{MB}} = \frac{\text{BC}}{\text{BN}} = \frac{\text{AC}}{\text{MN}} = k\]
\[\frac{a}{a - x} = \frac{b}{x}\]
\[ax = ab - bx\]
\[(a + b)x = ab\]
\[x = \frac{\text{ab}}{a + b}\]
\[MN = AM = \frac{\text{ab}}{a + b}.\]
\[\mathbf{Ответ:}а)\ MN = AP = 7,5\ см;\]
\[AM = NP = 5\ см;\]
\[\textbf{б)}\ MN = AP = AM = NP =\]
\[= \frac{\text{ab}}{a + b}.\]
