Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 623
Задание 623
\[\boxed{\mathbf{623.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - прямоугольная\ \]
\[трапеция;\]
\[\angle A = \angle B = 90{^\circ};\]
\[\angle ACD = 90{^\circ};\]
\[BC = 4\ см;\]
\[AD = 16\ см.\]
\[\mathbf{Найти:}\]
\[\angle C - ?\ \]
\[\angle D - ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}ACD\ \]
\[(по\ двум\ углам):\]
\[\angle B = \angle ACD = 90{^\circ}\ \]
\[(прямоугольные\ треугольники);\]
\[\angle BCA = \angle CAD\ \]
\[(как\ накрестлежащие).\]
\[Отсюда\]
\[\frac{\text{AD}}{\text{AC}} = \frac{\text{CD}}{\text{AB}} = \frac{\text{AC}}{\text{BC}} = k\]
\[\ \frac{16}{\text{AC}} = \frac{\text{CD}}{\text{AB}} = \frac{\text{AC}}{4}.\]
\[2)\frac{16}{\text{AC}} = \frac{\text{AC}}{4}:\]
\[AC^{2} = 16 \bullet 4\]
\[AC = \sqrt{64} = 8\ см.\]
\[3)\ CH = \sqrt{8^{2} - 4^{2}} =\]
\[= \sqrt{64 - 16} = \sqrt{48} = 4\sqrt{3}\ см.\]
\[4)\ HD = AD - AH = 16 - 4 =\]
\[= 12\ см.\]
\[5)\ CD = \sqrt{CH^{2} + HD^{2}} =\]
\[= \sqrt{\left( 4\sqrt{3} \right)^{2} + 12^{2}} =\]
\[= \sqrt{48 + 144} = \sqrt{192} =\]
\[= \sqrt{16 \bullet 4 \bullet 3} = \sqrt{64 \bullet 3} =\]
\[= 8\sqrt{3}\ см.\]
\[6)\ CH = \frac{1}{2}\text{CD}\]
\[4\sqrt{3} = \frac{1}{2} \bullet 8\sqrt{3} \Longrightarrow \ \]
\[7)\ \angle C + \angle D = 180{^\circ}\ \]
\[(как\ односторонние):\]
\[\angle C = 180{^\circ} - 30{^\circ} = 150{^\circ}\]
\[\mathbf{Ответ:\ }\angle C = 150{^\circ};\ \angle D = 30{^\circ}.\]
\[\boxed{\mathbf{623.еуроки - ответы\ на\ пятёрку}}\]
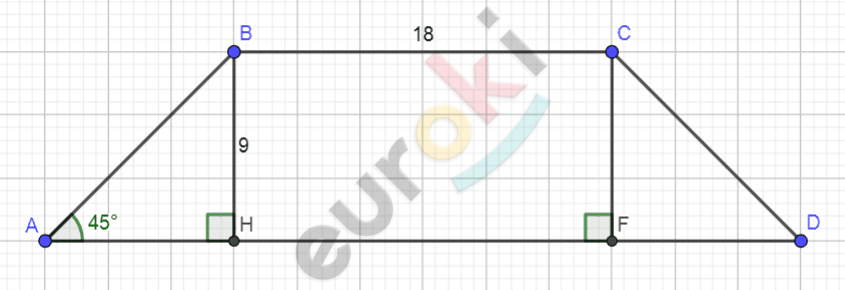
\[\mathbf{а)\ }Рисунок\ по\ условию\mathbf{\ задачи:\ \ }\]
\[\mathbf{Дано:}\]
\[ABCD - равнобедренная\ \]
\[трапеция;\]
\[BC = 18\ см;\]
\[BH = 9\ см;\]
\[\angle A = 45{^\circ}.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABCD}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ ⊿AHB - прямоугольный:\]
\[\angle ABH = 90{^\circ} - 45{^\circ} = 45{^\circ};\]
\[⊿AHB - равнобедренный;\]
\[AH = HB = 9\ см.\]
\[2)\ ABCD - равнобедренная\ \]
\[трапеция:\]
\[AB = CD;\ \]
\[3)\ ⊿ABH = ⊿CFD - по\ \]
\[гипотенузе\ и\ острому\ углу:\]
\[\angle A = \angle D;\ \]
\[AB = CD.\]
\[4)\ AD = AH + HF + FD =\]
\[= 9 + 18 + 9 = 36\ см.\]
\[5)\ S_{\text{ABCD}} = \frac{1}{2}(18 + 36) \bullet 9 =\]
\[= 243\ см^{2}.\]
\[Ответ:243\ см^{2}.\]
\[\mathbf{б}\mathbf{)\ Рисунок\ по\ условию\ задачи:}\]
\[\mathbf{Дано:}\]
\[ABCD - р/б\ трапеция;\]
\[BC = 16\ см;\]
\[AD = 30\ см;\]
\[AC\bot BD.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABCD}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ ABCD - равнобедренная\ \]
\[трапеция:\]
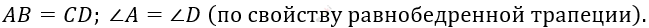
\[2)\ \mathrm{\Delta}ABD = \mathrm{\Delta}ACD - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[\angle A = \angle D;\]
\[AB = CD;\]
\[AD - общая.\]
\[Соответствующие\ элементы\ \]
\[в\ равных\ фигурах\ равны:\]
\[BD = AC;\]
\[\angle ABD = \angle ACD.\]
\[3)\ \mathrm{\Delta}ABO = \mathrm{\Delta}COD - по\ стороне\ \]
\[и\ двум\ прилежащим\ углам:\]
\[\angle BAO = \angle CDO\ \]
\[(так\ как\ \angle A = \angle D);\ \]
\[\angle ABD = \angle ACD;\]
\[AB = CD.\ \]
\[Соответствующие\ элементы\ \]
\[в\ равных\ фигурах\ равны:\]
\[BO = OC;\ \]
\[AO = OD.\ \]
\[4)\ \mathrm{\Delta}BOC - прямоугольный.\]
\[Пусть\ BO = OC = x;\]
\[BC^{2} = x^{2} + x^{2}\]
\[256 = 2x^{2}\]
\[x^{2} = 128\]
\[x = 8\sqrt{2}\ см.\]
\[5)\ \mathrm{\Delta}AOD - прямоугольный.\]
\[Пусть\ AO = OD = y;\]
\[AD^{2} = y^{2} + y^{2}.\]
\[900 = 2y^{2}\]
\[y^{2} = 450\]
\[y = 15\sqrt{2}\ см.\]
\[6)\ S_{\text{ABCD}} =\]
\[= S_{\text{ABO}} + S_{\text{COD}} + S_{\text{BOC}} + S_{\text{AOD}}.\]
\[7)\ S_{\text{ABO}} = S_{\text{COD}} =\]
\[= \frac{1}{2} \bullet 8\sqrt{2} \bullet 15\sqrt{2} = 120\ см^{2}.\]
\[8)\ S_{\text{AOD}} = \frac{1}{2} \bullet 15\sqrt{2} \bullet 15\sqrt{2} =\]
\[= 225\ см^{2}.\]
\[9)\ S_{\text{BOC}} = \frac{1}{2} \bullet 8\sqrt{2} \bullet 8\sqrt{2} =\]
\[= 64\ см^{2}.\]
\[10)\ S_{\text{ABCD}} =\]
\[= 120 + 120 + 225 + 64 =\]
\[= 529\ см^{2}.\]
\[Ответ:529\ см^{2}.\]
