Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 61
Задание 61
\[\boxed{\mathbf{61.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[hk\ и\ kl - смежные\ углы;\]
\[\textbf{а)}\ \angle hk = \angle kl - 40{^\circ}\]
\[\textbf{б)}\ \angle hk = \angle kl + 120{^\circ}\]
\[\textbf{в)}\ \angle hk = \angle kl + 47{^\circ}18'\]
\[\textbf{г)}\ \angle hk = 3\angle\text{kl}\]
\[\textbf{д)}\ \angle hk\ :\angle kl = 5\ :4\]
\[Найти:\]
\[\angle hk - ?\]
\[\angle kl - ?\]
\[Решение.\]
\[Сумма\ смежных\ углов\ \]
\[равна\ 180{^\circ}:\]
\[\angle hk + \angle kl = 180{^\circ}.\]
\[\textbf{а)}\ Пусть\ \angle\text{hk} = x,\ \]
\[тогда\ \angle kl = x + 40{^\circ}.\]
\[Составим\ уравнение:\]
\[x + x + 40{^\circ} = 180{^\circ}\ \]
\[2x = 140{^\circ}\]
\[x = \frac{140{^\circ}}{2}\]
\[x = 70{^\circ}.\]
\[\angle hk = 70{^\circ};\ \ \ \ \ \]
\[\angle kl = 70{^\circ} + 40{^\circ} = 110{^\circ}.\]
\[Ответ:70{^\circ}\ и\ 110{^\circ}.\]
\[\textbf{б)}\ Пусть\ \angle\text{kl} = x,\ \]
\[тогда\ \angle hk = x + 120{^\circ}.\]
\[Составим\ уравнение:\]
\[x + x + 120{^\circ} = 180{^\circ}\]
\[2x = 60{^\circ}\]
\[x = \frac{60{^\circ}}{2}\]
\[x = 30{^\circ}.\]
\[\angle kl = 30{^\circ};\ \ \]
\[\ \angle hk = 30{^\circ} + 120{^\circ} = 150{^\circ}.\]
\[Ответ:30{^\circ}\ и\ 150{^\circ}.\]
\[\textbf{в)}\ Пусть\ \angle\text{kl} = x,\]
\[\ тогда\ \angle hk = x + 47{^\circ}18^{'}.\]
\[Составим\ уравнение:\]
\[x + x + 47{^\circ}18^{'} = 180{^\circ}\]
\[2x = 132{^\circ}42'\]
\[x = \frac{132{^\circ}42^{'}}{2}\]
\[x = 66{^\circ}21'\]
\[\angle kl = 66{^\circ}21^{'};\ \ \ \]
\[\angle hk = 66{^\circ}21^{'} + 47{^\circ}18^{'} =\]
\[= 113{^\circ}39^{'}.\]
\[Ответ:66{^\circ}21^{'};\ \ 113{^\circ}39^{'}.\]
\[\textbf{г)}\ Пусть\ \angle\text{kl} = x,\ \]
\[тогда\ \angle hk = 3x.\]
\[Составим\ уравнение:\]
\[x + 3x = 180{^\circ}\]
\[4x = 180{^\circ}\]
\[x = \frac{180{^\circ}}{4}\]
\[x = 45{^\circ}.\]
\[\angle kl = 45{^\circ};\ \ \ \]
\[\angle hk = 45{^\circ} \bullet 3 = 135{^\circ}.\]
\[Ответ:45{^\circ}\ и\ 135{^\circ}.\]
\[\textbf{д)}\ Пусть\ \angle\text{kl} = 4x,\]
\[\ тогда\ \angle hk = 5x.\]
\[Составим\ уравнение:\]
\[4x + 5x = 180{^\circ}\]
\[9x = 180{^\circ}\]
\[x = \frac{180{^\circ}}{9}\]
\[x = 20{^\circ}.\]
\[\angle kl = 20{^\circ} \bullet 4 = 80{^\circ};\ \ \ \]
\[\angle hk = 20{^\circ} \bullet 5 = 100{^\circ}.\]
\[Ответ:80{^\circ}\ и\ 100{^\circ}.\]
\[\boxed{\mathbf{61.еуроки - ответы\ на\ пятёрку}}\]
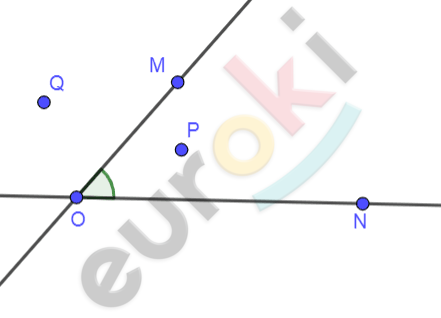
\[Построим\ угол\ MON,\ \]
\[обозначим\ точки\ \text{P\ }и\ Q:\]
\[Проведем\ перпендикулярные\ \]
\[прямые\]
