Решебник по геометрии 7 класс Атанасян ФГОС Задание 562

 

\[\boxed{\mathbf{562.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[AB = a;\]

\[CH = h;\]

\[CH\bot AB;\]

\[MNFE - квадрат.\]

\[\mathbf{Найти:}\]

\[MN - ?\]

\[\mathbf{Решение.}\]

\[1)\ NF \parallel AB\ и\ CA - секущая:\]

\[\angle CNF = \angle CAB\ \]

\[(как\ соответственные).\]

\[2)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}NCF\ \]

\[(по\ двум\ углам):\]

\[\angle C - общий;\ \]

\[\angle CNF = \angle CAB.\]

\[Отсюда:\]

\[\frac{\text{AB}}{\text{NF}} = \frac{\text{CH}}{\text{CQ}}.\]

\[3)\ MNFE - квадрат:\]

\[MN = NF = FE = ME = x.\]

\[4)\ Получаем:\ \]

\[CQ = h - x.\]

\[5)\ \frac{a}{x} = \frac{h}{h - x}\]

\[ah - ax = hx\]

\[ah = (a + h)x\]

\[x = \frac{\text{ah}}{a + h}\]

\[MN = \frac{\text{ah}}{a + h}.\]

\[\mathbf{Ответ:}MN = \frac{\text{ah}}{a + h}\mathbf{.}\]

\[\boxed{\mathbf{562.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[\angle A = 45{^\circ};\]

\[AB = 15,2\ см;\]

\[BD - диагональ;\]

\[BD = AD.\]

\[\mathbf{Найти:}\]

\[S_{\text{ABCD}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ AD = BD\ (по\ условию):\]

\[\mathrm{\Delta}ADB - равнобедренный.\]

\[Получаем6\]

\[\angle ABD = \angle DAB = 45{^\circ} \Longrightarrow\]

\[\Longrightarrow \angle BDA = 90{^\circ}.\]

\[2)\ Проведем\ DH - медиану\ \]

\[к\ \text{AB}\text{:}\ \]

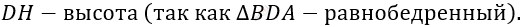
\[3)\ По\ свойству\ медианы\ в\ \]

\[равнобедренном\ треугольнике:\ \]

\[DH = \frac{1}{2}AB = \frac{1}{2} \bullet 15,2 = 7,6\ см.\]

\[4)\ S_{\text{ABCD}} = AB \bullet DH =\]

\[= 15,2 \bullet 7,6 = 115,52\ см^{2}.\]

\[Ответ:115,52\ см^{2}.\]