Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 543
Задание 543
\[\boxed{\mathbf{543.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
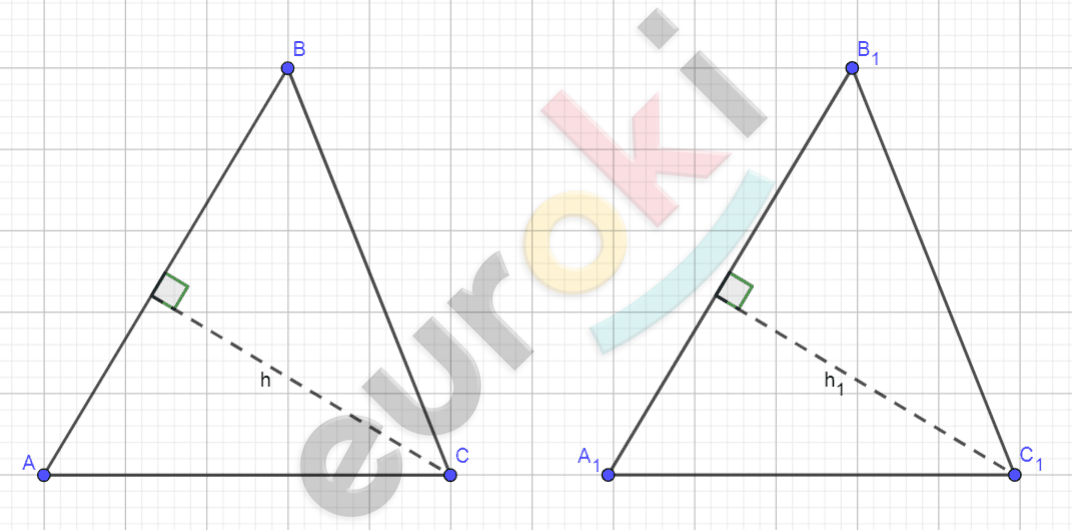
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC}\sim\mathrm{\Delta}A_{1}B_{1}C_{1};\]
\[\text{AB}\ :A_{1}B_{1} = k.\]
\[\mathbf{Доказать:}\]
\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{h}{h_{1}}.\]
\[\mathbf{Доказательство.}\]
\[1)\ По\ теореме\ об\ отношении\ \]
\[площадей\ подобных\ \]
\[треугольников:\]
\[\frac{S_{\text{ABC}}}{S_{A_{1}B_{1}C_{1}}} = k^{2}.\]
\[2)\frac{\frac{1}{2}\text{AB} \bullet h}{\frac{1}{2} \bullet A_{1}B_{1} \bullet h^{1}} = k^{2}\]
\[\frac{\text{AB}}{A_{1}B_{1}} \bullet \frac{h}{h^{1}} = k^{2}\]
\[k \bullet \frac{h}{h_{1}} = k^{2}\]
\[\frac{h}{h_{1}} = k \Longrightarrow \frac{\text{AB}}{A_{1}B_{1}} = \frac{h}{h_{1}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{543.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[CM = DC.\]
\[\mathbf{Доказать:}\]
\[S_{\text{ABCD}} = S_{\text{AMD}}.\]
\[\mathbf{Доказательство.}\]
\[1)\ AB \parallel MD\ и\ AM - секущая:\]
\[\angle CMA = \angle BAO\ \]
\[(как\ накрестлежащие);\]
\[\angle\text{ABO} = \angle MCO\ \]
\[(как\ накрестлежащие),\ \]
\[AB = MC\ \]
\[(так\ как\ MC = CD\ и\ AB = CD),\ \]
\[Получаем:\]
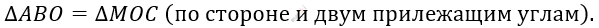
\[2)\ S_{\text{ABCD}} = S_{\text{ABO}} + S_{\text{AOCD}};\ \ \]
\[S_{\text{AMD}} = S_{\text{MOC}} + S_{\text{AOCD}};\]
\[S_{\text{ABO}} = S_{\text{MOC}}\ \]
\[(так\ как\ фигуры\ равны).\]
\[Следовательно:\]
\[S_{\text{ABCD}} = S_{\text{AMD}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
