Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 480
Задание 480
\[\boxed{\mathbf{480.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[\text{ABCD} - трапеция;\]
\[\text{AB} = 21\ см;\]
\[\text{BH} = 7\ см;\]
\[\text{CD} = 17\ см.\]
\[Найти:\]
\[S_{\text{ABCD}} - ?\]
\[Решение.\]
\[S_{\text{ABCD}} = \frac{1}{2} \bullet \left( \text{AB} + \text{CD} \right) \bullet \text{BH} =\]
\[= \frac{1}{2} \bullet (21 + 17) \bullet 7 = 19 \bullet 7 =\]
\[= 133\ см^{2}.\]
\[\textbf{б)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[\text{ABCD} - трапеция;\]
\[\angle D = 30{^\circ};\]
\[\text{AB} = 2\ см;\]
\[\text{CD} = 10\ см;\]
\[\text{DA} = 8\ см;\]
\[Найти:\]
\[S_{\text{ABCD}} - ?\]
\[Решение.\]
\[1)\ Рассмотрим\ ⊿\text{AED}:\]
\[2)\ S_{\text{ABCD}} = \frac{1}{2}\left( \text{AB} + \text{CD} \right) \bullet \text{AE} =\]
\[= \frac{1}{2}(2 + 10) \bullet 4 = \frac{1}{2} \bullet 12 \bullet 4 =\]
\[= 24\ см^{2}.\]
\[\textbf{в)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[\text{ABCD} - трапеция;\]
\[\text{BC}\bot\text{AB};\]
\[\text{AB} = 5\ см;\]
\[\text{CD} = 13\ см;\]
\[\text{BC} = 8\ см.\]
\[Найти:\]
\[S_{\text{ABCD}} - ?\]
\[Решение.\]
\[1)\ \text{BC} - высота\ \]
\[\left( так\ как\ \text{BC}\bot\text{AB} \right).\]
\[2)\ S_{\text{ABCD}} = \frac{1}{2}\left( \text{AB} + \text{CD} \right) \bullet \text{BC} =\]
\[= \frac{1}{2}(5 + 13) \bullet 8 = \frac{1}{2} \bullet 18 \bullet 8 =\]
\[= 72\ см^{2}.\]
\[Ответ:а)\ 133\ см^{2};б)\ 24\ см^{2};\]
\[\textbf{в)}\ 72\ см^{2}.\]
\[\boxed{\mathbf{480.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Рисунок\ по\ условию\ задачи:}\]
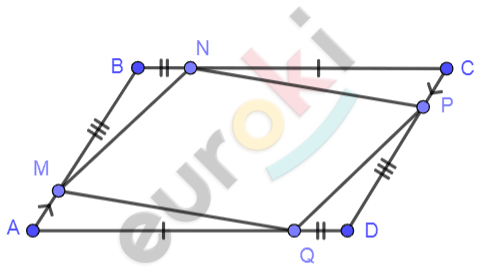
\[\mathbf{Дано:}\]
\[ABCD - четырехугольник;\]
\[AM = CP;\]
\[BN = DQ;\]
\[BM = DP;\]
\[NC = QA.\]
\[\mathbf{Доказать:}\]
\[\text{ABCD\ }и\ MNPQ -\]
\[параллелограммы.\]
\[\mathbf{Доказательство.}\]
\[1)\ BC = BN + NC;\ \]
\[AD = QD + AQ;\]
\[BN = QD;\ \ \ \]
\[NC = QA.\]
\[Получаем:\]
\[BC = AD.\]
\[2)\ AB = BM + MA;\ \]
\[CD = PD + CP\]
\[AM = CP;\ \ \ \]
\[BM = DP.\]
\[Получаем:\]
\[AB = CD.\]
\[6)\ Соответствующие\ элементы\ \]
\[в\ равных\ фигурах\ равны:\ \]
\[MN = PQ;\]
\[MQ = NP.\]
\[7)\ По\ второму\ признаку\]
\[параллелограмма:\ \]
\[MNPQ - параллелограмм.\]
\[Что\ и\ требовалось\ доказать.\]
