Решебник по геометрии 7 класс Атанасян ФГОС Задание 452

 

\[\boxed{\mathbf{452.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[S - площадь\ прямоугольника;\]

\[a\ и\ b - стороны\ \]

\[прямоугольника;\]

\[S = a \bullet b;\]

\[a = S\ :b;\]

\[b = S\ :a.\]

\[\textbf{а)}\ a = 8,5\ см;b = 3,2\ см:\]

\[S = 8,5 \bullet 3,2 = 27,2\ см^{2}.\]

\[\textbf{б)}\ a = 2\sqrt{2}\ см;b = 3\ см:\]

\[S = 2\sqrt{2} \bullet 3 = 6\sqrt{2}\ см^{2}.\]

\[\textbf{в)}\ S = 684,8\ см^{2};a = 32\ см:\]

\[b = 684,8\ :32 = 21,4\ см.\]

\[\textbf{г)}\ S = 12,5\ см^{2};b = 4,5\ см:\]

\[a = 12,5\ :4,5 = 2,7\ см.\]

\[\boxed{\mathbf{452.еуроки - ответы\ на\ пятёрку}}\]

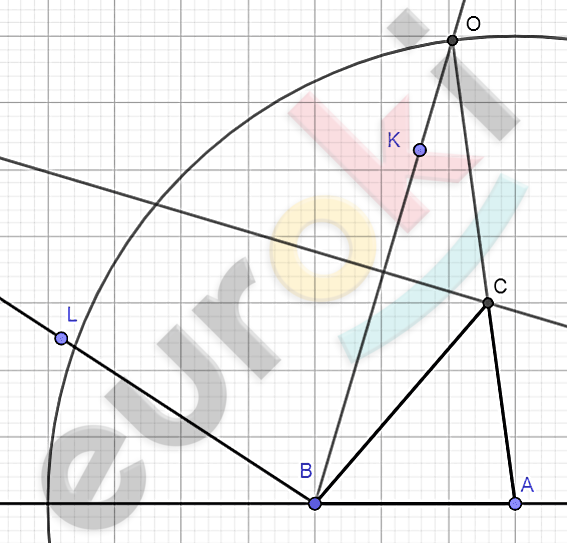
\[Дано:\]

\[s = |BC - AC|;\]

\[\angle M = |\angle A - \angle B|.\]

\[Построить:\ \]

\[\mathrm{\Delta}\text{ABC.}\]

\[Построение.\]

\[1)\ Построим\ \angle B = \angle M.\]

\[На\ одной\ стороне\ угла\ \text{B\ }\]

\[отметим\ точку\ L,\]

\[вторую\ сторону\ продолжим\ \]

\[через\ точку\ \text{B.}\]

\[2)\ На\ продолжении\ стороны\ \]

\[отложим\ отрезок\ \text{BA.}\]

\[3)\ Построим\ биссектрису\ \]

\[\angle LBA - BK.\]

\[4)\ Построим\ окружность\ (A;s),\ \]

\[на\ пересечении\ с\ \text{BK\ }отметим\ \]

\[точку\ O.\]

\[5)\ Построим\ серединный\ \]

\[перпендикуляр\ отрезка\ BO,\ \]

\[на\ пересечении\ с\ \]

\[отрезком\ \text{AO\ }отметим\ точку\ \text{C.}\]