Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 430
Задание 430
\[\boxed{\mathbf{430.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\text{ABCD} - выпуклый\ \]
\[четырехугольник;\]
\[\angle A = \angle C;\]
\[\angle B = \angle D.\]
\[\mathbf{Доказать:}\]
\[\text{ABCD} - параллелограмм.\]
\[\mathbf{Доказательство.}\]
\[1)\ По\ свойству\ суммы\ углов\ в\ \]
\[четырехугольнике:\]
\[\angle A + \angle B + \angle C + \angle D = 360{^\circ}.\]
\[2)\ \angle A = \angle C;\ \ \ \angle B = \angle D:\]
\[2\angle A + 2\angle B = 360{^\circ}\]
\[\angle A + \angle B = 180{^\circ}\]
\[\angle A = \angle C.\]
\[Следовательно:\ \]
\[\angle C + \angle B = 180{^\circ}.\]
\[1)\ \angle A + \angle B = 180{^\circ};\]
\[\angle A\ и\ \angle B - односторонние;\]
\[следовательно:\]
\[\text{BC} \parallel \text{AD}.\]
\[2)\ \angle B + \angle C = 180{^\circ};\]
\[\angle B\ и\ \angle C - односторонние;\]
\[следовательно:\]
\[\text{CD} \parallel \text{AB}.\]
\[3)\ По\ определению\ \]
\[параллелограмма:\]
\[\text{ABCD} - параллелограмм.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{430.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
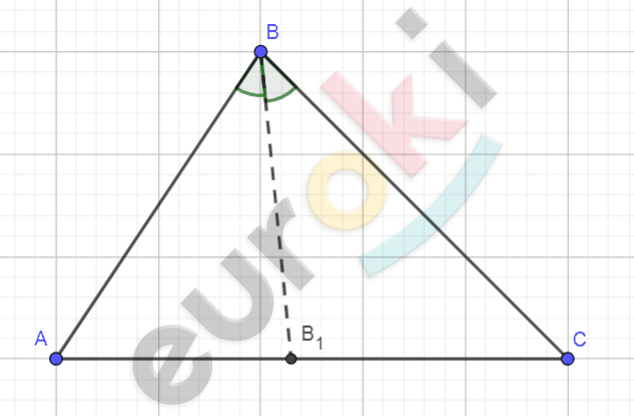
\[BB_{1} - биссектриса.\]
\[\mathbf{Доказать:}\]
\[BA > B_{1}A,\ \]
\[BC > B_{1}\text{C.}\]
\[\mathbf{Доказательство.}\]
\[1)\ \angle ABB_{1} = \angle B_{1}\text{BC\ }\]
\[\left( так\ как\ BB_{1} - биссектриса \right).\]
\[2)\ По\ свойству\ внешнего\ угла:\ \]
\[\angle BB_{1}A = \angle B_{1}BC + \angle BCB_{1}.\]
\[Отсюда:\ \]
\[\angle BB_{1}A > \angle B_{1}\text{BC\ }и\ \]
\[\angle BB_{1}A > \angle ABB_{1}.\]
\[3)\ Рассмотрим\ \mathrm{\Delta}\text{AB}B_{1}:\]
\[\angle BB_{1}\text{A\ }лежит\ против\ \text{AB\ }и\ \]
\[\angle ABB_{1}\ лежит\ против\ AB_{1};\]
\[\angle BB_{1}A > \angle ABB_{1} \Longrightarrow AB > AB_{1}.\]
\[4)\ По\ свойству\ внешнего\ угла:\ \]
\[\angle BB_{1}C = \angle ABB_{1} + \angle BAB_{1}.\]
\[Отсюда:\ \]
\[\angle BB_{1}C > \angle ABB_{1}\ и\ \]
\[\angle BB_{1}C > \angle B_{1}\text{BC.}\]
\[5)\ Рассмотрим\ \mathrm{\Delta}\text{BC}B_{1}:\]
\[\angle BB_{1}\text{C\ }лежит\ против\ \text{BC\ }и\ \]
\[\angle B_{1}\text{BC\ }лежит\ против\ B_{1}C;\]
\[\angle BB_{1}C > \angle B_{1}BC \Longrightarrow \ BC > B_{1}\text{C.}\]
\[Что\ и\ требовалось\ доказать.\]
