Решебник по геометрии 7 класс Атанасян ФГОС Задание 399

 

\[\boxed{\mathbf{399.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[\angle A = 90{^\circ}.\]

\[\mathbf{Доказать:}\]

\[ABCD - прямоугольник.\]

\[\mathbf{Доказательство.}\]

\[1)\ По\ свойству\ \]

\[параллелограмма:\]

\[AB = CD,\ BC = AD,\ BC \parallel AD,\ \]

\[AB \parallel CD.\]

\[2)\ BC \parallel AD\ и\ AB - секущая:\]

\[\angle A + \angle B =\]

\[= 180{^\circ}\ (как\ односторонние);\]

\[\angle B = 180{^\circ} - 90{^\circ} = 90{^\circ}.\]

\[3)\ По\ свойству\ \]

\[параллелограмма:\]

\[\angle A = \angle D = 90{^\circ};\]

\[\ \angle B = \angle C = 90{^\circ}.\]

\[По\ определению\ \]

\[прямоугольника:\]

\[ABCD - прямоугольник.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{399.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - вписанный;\]

\[Окр\ (O;r);\]

\[O \in медиане.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}ABC - равнобедренный\ или\ \]

\[прямоугольный.\]

\[\mathbf{Доказательство.}\]

\[\textbf{а)}\ \]

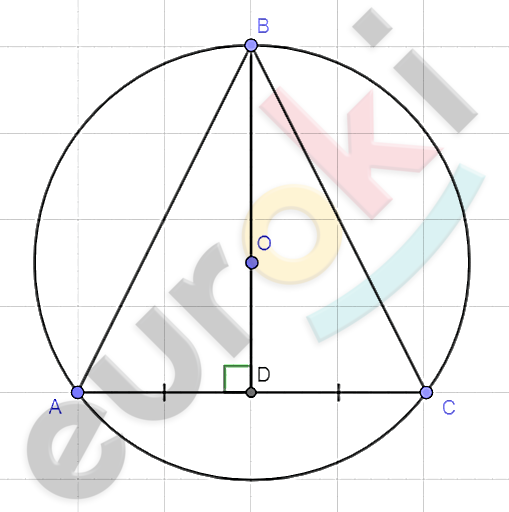
\[1)\ По\ условию\ центр\ O\ \]

\[описанной\ окружности\ лежит\]

\[на\ медиане\ BD,\ но\ центр\ \]

\[описанной\ окружности\ точка\]

\[пересечения\ серединных\ \]

\[перпендикуляров.\]

\[Значит:\ \]

\[BD - медиана\ и\ серединный\ \]

\[перпендикуляр.\]

\[Отсюда:\ \]

\[\angle ADB = \angle CDB = 90{^\circ}.\]

\[2)\ \mathrm{\Delta}ABD = \mathrm{\Delta}BCD\ \]

\[(по\ двум\ катетам):\]

\[AD = DC;\ \]

\[BD - общий\ катет.\]

\[Отсюда:\ \]

\[AB = BC.\]

\[3)\ Значит:\ \]

\[\mathrm{\Delta}ABC - равнобедренный\ \]

\[по\ определению.\]

\[\textbf{б)}\ \]

\[1)\ Центр\ описанной\ \]

\[окружности\ совпадает\ \]

\[с\ основанием\ медианы \Longrightarrow\]

\[\Longrightarrow CO - медиана\ \mathrm{\Delta}\text{ABC.}\]

\[2)\ Значит:\ \]

\[\angle\text{ACB\ }опирается\ на\ диаметр\ и\ \]

\[равен\ 90{^\circ}.\]

\[Следовательно:\ \]

\[\mathrm{\Delta}ABC - прямоугольный.\]

\[Что\ и\ требовалось\ доказать.\]