Решебник по геометрии 7 класс Атанасян ФГОС Задание 361

 

\[\boxed{\mathbf{361.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[P - периметр\ \mathrm{\Delta}ABC.\]

\[Построить:\ \]

\[\mathrm{\Delta}ABC.\]

\[Построение.\]

\[1)\ Из\ данных\ углов\ построим\ \]

\[любой\ треугольник\ AB_{1}C_{1}.\]

\[2)\ Построим\ любой\ угол\ \text{M\ }и\ \]

\[отметим\ на\ одной\ из\ его\ \]

\[сторон\ отрезок\ MP = P.\]

\[3)\ На\ второй\ стороне\ угла\ \text{M\ }\]

\[отложим\ последовательно\ \]

\[отрезки,равные\ AC_{1},\ AB_{1}\ и\ \]

\[C_{1}B_{1}.\ На\ конце\ отметим\ \]

\[точку\ P_{1}.\]

\[4)\ Проведем\ отрезок\ PP_{1},\ а\ \]

\[затем\ через\ другие\ точки,\ \]

\[лежащие\ на\ MP_{1},\ прямые,\ \]

\[параллельные\ отрезку\ PP_{1}\text{.\ }На\ \]

\[пересечении\ прямых\]

\[и\ второй\ стороны\ угла\ отметим\ \]

\[точки\ C^{'}\ и\ B^{'}.\]

\[5)\ Получаем:\]

\[MC^{'} = AC,\ C^{'}B^{'} = AB\ и\ \]

\[BP = BC;\]

\[так\ как\ отрезки\]

\[\frac{\text{AC}}{AC_{1}} = \frac{\text{BC}}{BC_{1}} = \frac{\text{AB}}{AB_{1}} = \frac{P_{\text{ABC}}}{P_{AB_{1}C_{1}}}.\]

\[6)\ На\ стороне\ AC_{1}\ угла\ \text{A\ }\]

\[отложим\ отрезок\ AC = MC^{'},\ \]

\[а\ на\ стороне\ AB_{1} - \ отрезок\ \]

\[AB = C^{'}B^{'}.\]

\[\boxed{\mathbf{361.еуроки - ответы\ на\ пятёрку}}\]

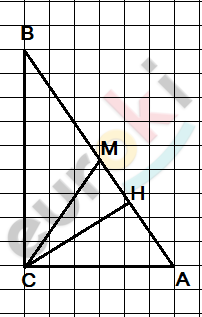
\[Сначала\ построим\ \]

\[прямоугольный\ ⊿CHM:\]

\[h - катет;m - гипотенуза;\ \]

\[\angle H = 90{^\circ}.\]

\[1)\ На\ \text{HM\ }слева\ и\ справа\ \]

\[от\ точки\ \text{M\ }отложим\ \]

\[MB = MA = m.\]

\[2)\ Соединим\ точки\ A;B;C.\]

\[3)\ \angle MCB = \angle MBC = \angle 1;\ \ \]

\[\angle CAM = \angle ACM = 2;\]

\[так\ как\ ⊿CMB\ и\ ⊿ACM -\]

\[равнобедренные.\]

\[4)\ ⊿ACB - искомый.\]