Решебник по геометрии 7 класс Атанасян ФГОС Задание 346

 

\[\boxed{\mathbf{346.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[AB < AC;\]

\[AD - биссектриса;\]

\[AH - высота.\]

\[\mathbf{Доказать:}\]

\[H \in DB.\]

\[\mathbf{Доказательство.}\]

\[1)\ AB < AC\ (по\ условию):\ \]

\[2)\ \angle ADB + \angle ADC =\]

\[= 180{^\circ}\ (как\ смежные):\]

\[\angle ADB < 90{^\circ}\ и\ \angle ADC > 90{^\circ}.\]

\[3)\ \mathrm{\Delta}ADC - тупоугольный:\]

\[\text{H\ }лежит\ на\ продолжении\ \]

\[стороны\ \text{DC\ }\]

\[(задача\ №300) \Longrightarrow H \in DB.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{346.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

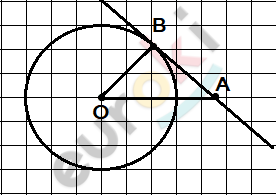
\[окружность\ (O;r);\]

\[r = 12\ см;\]

\[\angle AOB = 45{^\circ}.\]

\[Найти:\]

\[\text{AB}.\]

\[Решение.\]

\[Проведем\ радиус\ \]

\[окружности\ OB;соединим\ \]

\[точки\ \text{O\ }и\ \text{A.}\]

\[Получим\ треугольник\ AOB -\]

\[прямоугольный:\]

\[так\ как\ касательная\ \]

\[к\ окружности\ \bot к\ радиусу,\ \]

\[проведенному\ в\ точку\ касания.\]

\[⊿AOB - равнобедренный:\]

\[\angle BAO = \angle AOB = 45{^\circ}.\]

\[Следовательно:\]

\[AB = OB = 12\ см.\]

\[Ответ:12\ см.\]