Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 335
Задание 335
\[\boxed{\mathbf{335.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:\ }\]
\[\mathrm{\Delta}ABC.\ \]
\[Определить:\]
\[вид\ треугольника.\]
\[Решение.\]
\[\textbf{а)}\ Если\ сумма\ любых\ двух\ \]
\[углов\ больше\ 90{^\circ}:\]
\[\angle A + \angle B > 90{^\circ};\ \]
\[\angle B + \angle C > 90{^\circ};\ \]
\[\angle A + \angle C > 90{^\circ}.\]
\[Так\ как\ \angle A + \angle B + \angle C = 180{^\circ}\ \]
\[(по\ теореме\ о\ сумме\ углов),\ то\]
\[каждый\ из\ углов\ должен\ быть\ \]
\[меньше\ 90{^\circ},\ иначе\ сумма\ двух\ \]
\[других\ углов\ будет\ меньше\ \]
\[или\ равна\ 90{^\circ}.\]
\[Следовательно:\ \mathrm{\Delta}ABC -\]
\[остроугольный.\]
\[\textbf{б)}\ Каждый\ угол\ меньше\ суммы\ \]
\[двух\ других\ углов:\]
\[\angle A < \angle B + \angle C;\ \]
\[\angle B < \angle A + \angle C;\ \]
\[\angle C < \angle A + \angle B.\]
\[По\ теореме\ о\ сумме\ углов\ в\ \]
\[треугольнике:\]
\[\angle A + \angle B + \angle C = 180{^\circ}\ .\]
\[Следовательно:\]
\[каждый\ из\ углов\ должен\ быть\ \]
\[меньше\ 90{^\circ},\ так\ как\ в\ обратном\ \]
\[случае\ сумма\ трех\ углов\ будет\ \]
\[превышать\ 180{^\circ}.\]
\[Получаем:\ \ \]
\[\mathrm{\Delta}ABC - остроугольный.\]
\[Ответ:в\ обоих\ случаях\ \]
\[треугольник\ остроугольный.\]
\[\boxed{\mathbf{335.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
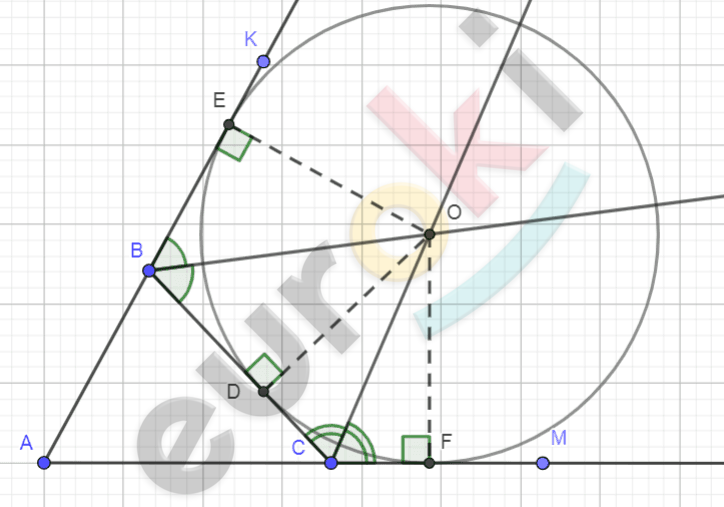
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[BO;CO - биссектрисы;\]
\[BO \cap CO = O.\]
\[\mathbf{Доказать:}\]
\[O - центр\ окружности;\]
\[AB,BC,AC - касательные.\]
\[\mathbf{Доказательство.}\]
\[1)\ BO - биссектриса\ \angle KBC:\]
\[\ OF\bot BK;\ \]
\[OD\bot BC;\]
\[OD = OE\ (по\ свойству\ биссектрис).\]
\[2)\ CO - биссектриса\ \angle BCM:\]
\[OD\bot BC;\]
\[OF\bot CM;\]
\[OD = OF\ (по\ свойству\ биссектрис).\]
\[3)\ OD = OE\ и\ OD = OF:\ \]
\[OE = OF = OD - радиус\ окружности\ с\ центром\ в\ точке\ \text{O.}\]
\[4)\ OE\bot BK;\ \ OD\bot BC;\ \ OF\bot CM:\]
\[AB;BC\ и\ AC - касательные\ к\ окружности.\ \]
\[Что\ и\ требовалось\ доказать.\]
